Match the following lists and then choosen the corrct code.
Solution in Tamil

1) $\begin{matrix} a & b & c & d q & p & s & r \end{matrix}$

2) $\begin{matrix} a & b & c & d q & r & s & q \end{matrix}$

3) $\begin{matrix} a & b & c & d s & p & q & r \end{matrix}$

4) $\begin{matrix} a & b & c & d q & q & s & p \end{matrix}$

Video Solution

Text Solution

Verified by Experts

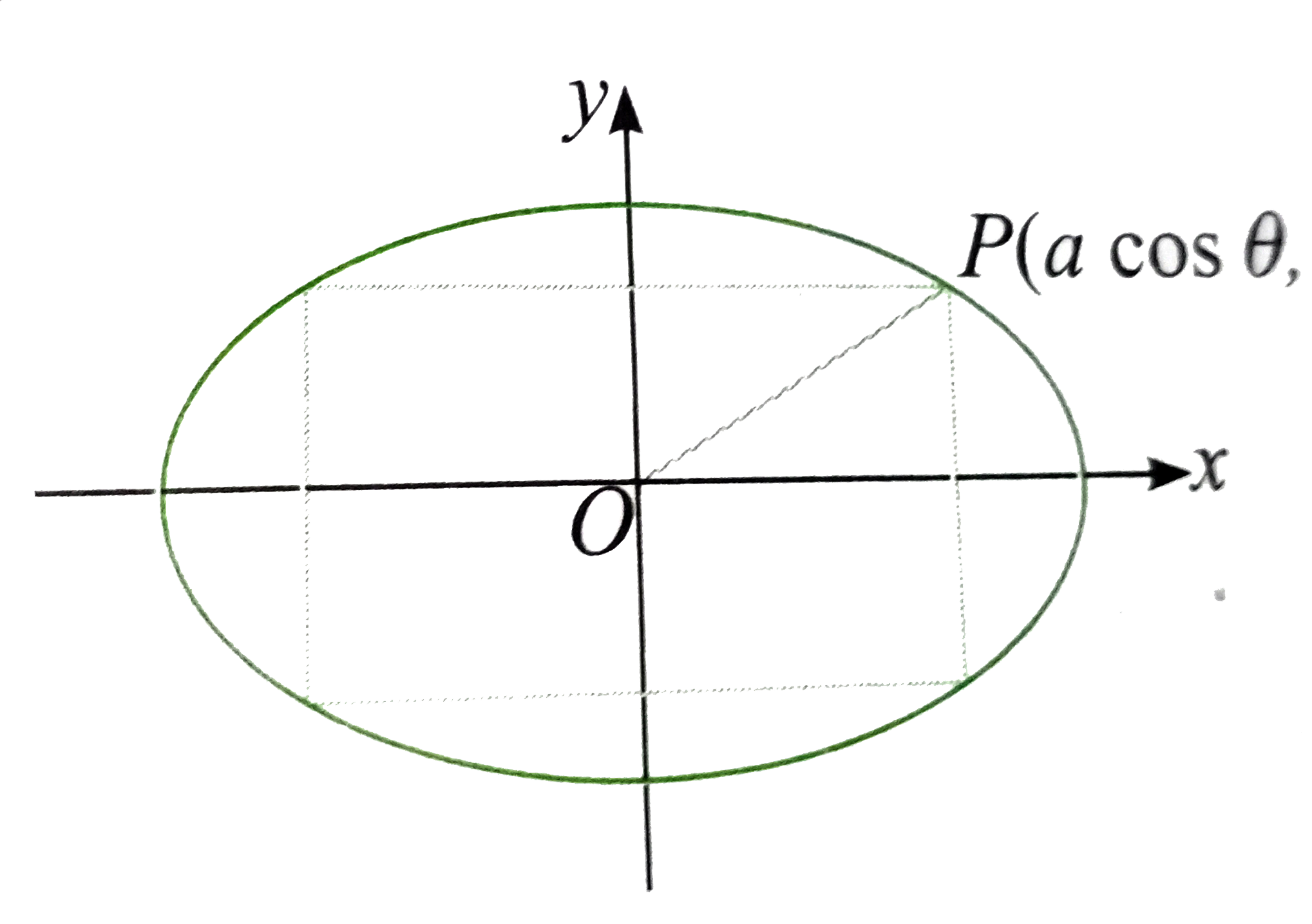
(a) Let one of the vertices of the rectangle be
$P (a cos θ, b sin θ)$ . Then its area is
$A = (2 a cos θ) (2 b sin θ) = 2 a b sin 2 θ$
Hence, $A_{max} = 2 a b$
Now, the area of recrtangle formed by the extermities of the latus rectum is
$2 a e \times \frac{2 b^{2}}{a} = 4 e b^{2}$
Given that
$2 a b = 4 e b^{2}$
or $\frac{2 b}{a} e = 1$
$or \frac{4 b^{2}}{a^{2}} e^{2} = 1$
or $4 (1 - e^{2}) e^{2} = 1$
$or {(2 e^{2} - 1)}^{2} = 0$
(b)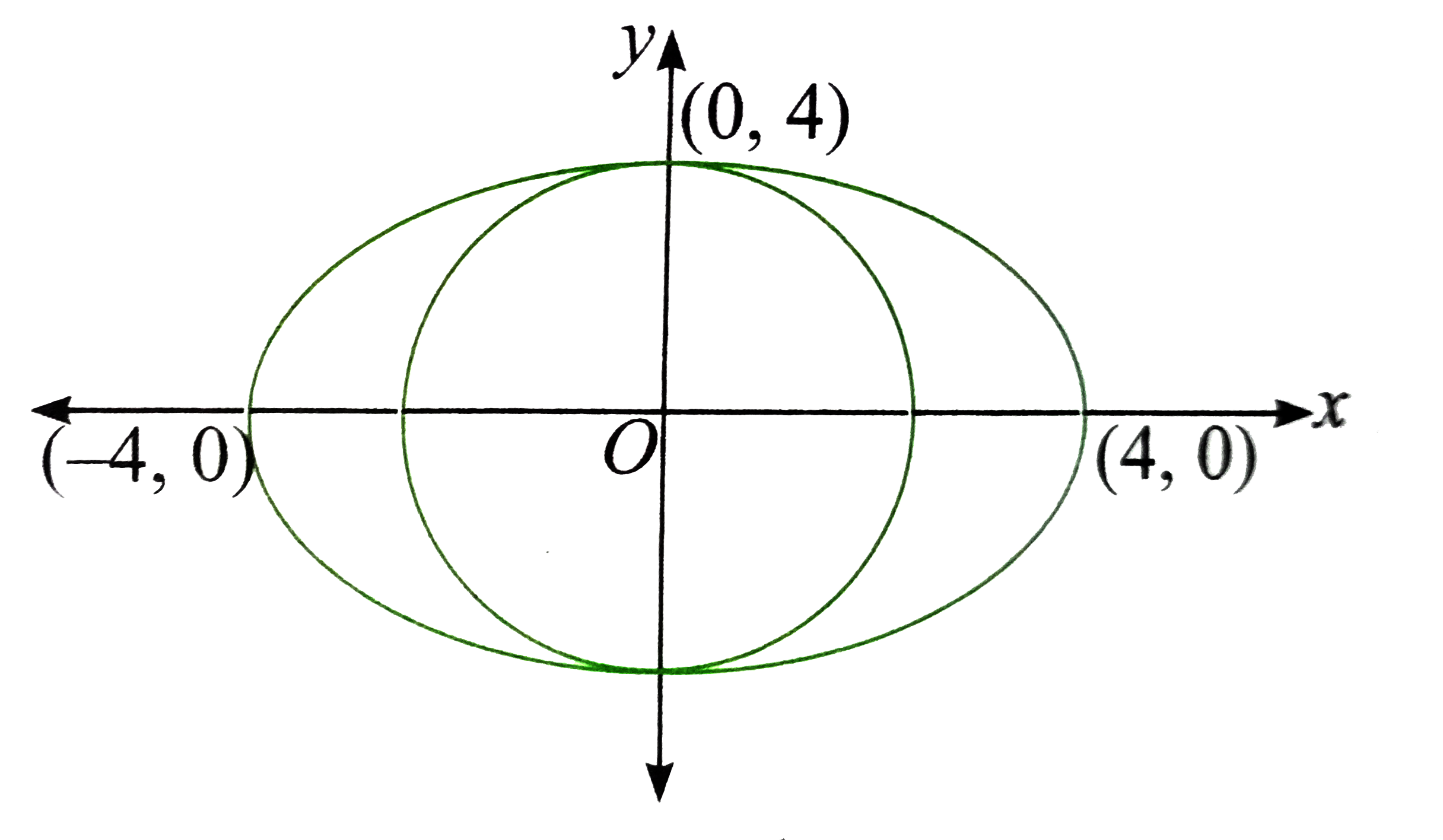
For the ellipse, the distacec between the foci, $2 a e = 8$ , and the length of the semi-minor axis is b=4 . Now,
$b^{2} = a^{2} - a^{2} e^{2}$
or $16 = a^{2} - 16$
$or e^{2} = 32$
or $e = \sqrt{1 - \frac{16}{32}} = \frac{1}{\sqrt{2}}$
(c) Normal at point P(6,2) to the ellipse passes through its focus Q(5,2). Then P must be the extermity of the major axis, Now, ae=QR=1 (where R is ceter ) and a-ae=1

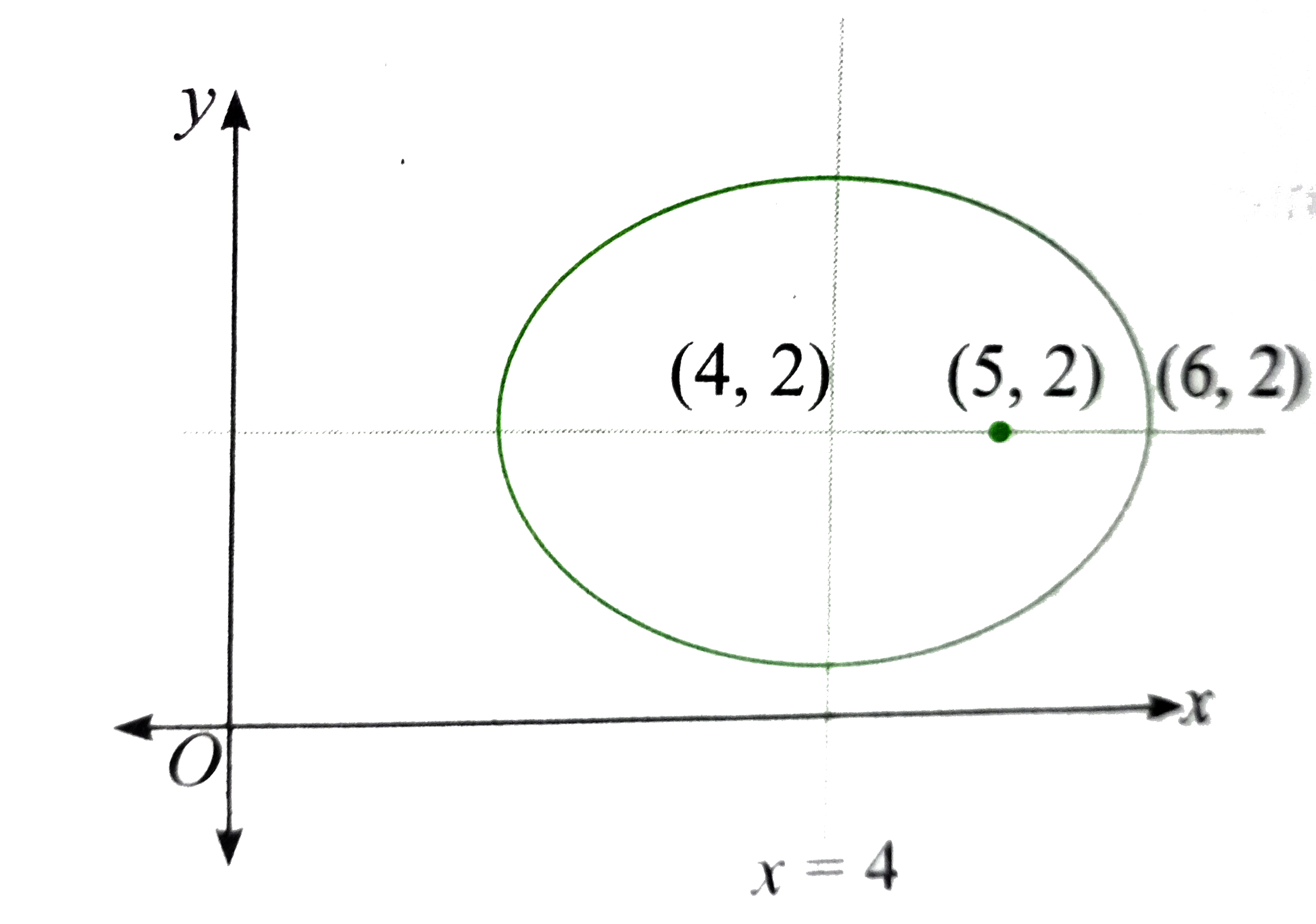
$∴ a = 2$
$b^{2} = a^{2} - a^{2} e^{2} = 4 - 1 = 3$
or $e = \sqrt{1 - \frac{3}{4}} = \frac{1}{2}$
(d)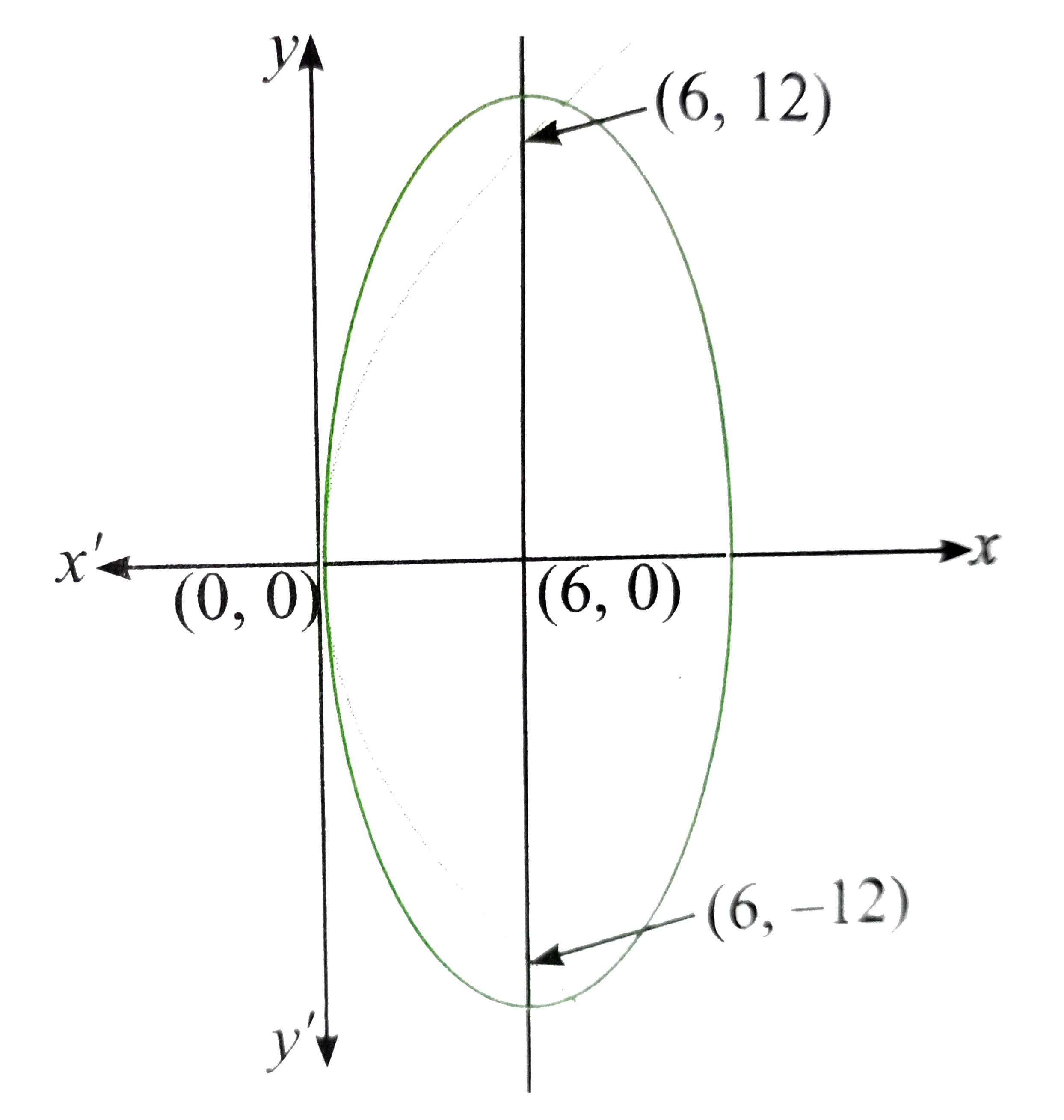
The extermities of the lotus rectum of teh parabola $y^{2} = 24 x$ are $(6, \pm 12)$ . For ellipse $2 b e = 24$ and the extermity of the minro axis is (0,0). Hence a=6. Now,
$a^{2} = b^{2} - b^{2} e^{2}$
or $b^{2} = 36 + 144 = 180$
or $e^{2} \sqrt{1 - \frac{36}{180}} = \sqrt{1 - \frac{1}{5}} = \frac{2}{\sqrt{5}}$

Updated on:21/07/2023