The area (in sq. units) of the quadrilateral formed by the tangents at the end points of the latera recta to the ellipse x29+y25=1
27/4
18
27/2
27
The correct Answer is:D
The given ellipe is
x29+y25=1
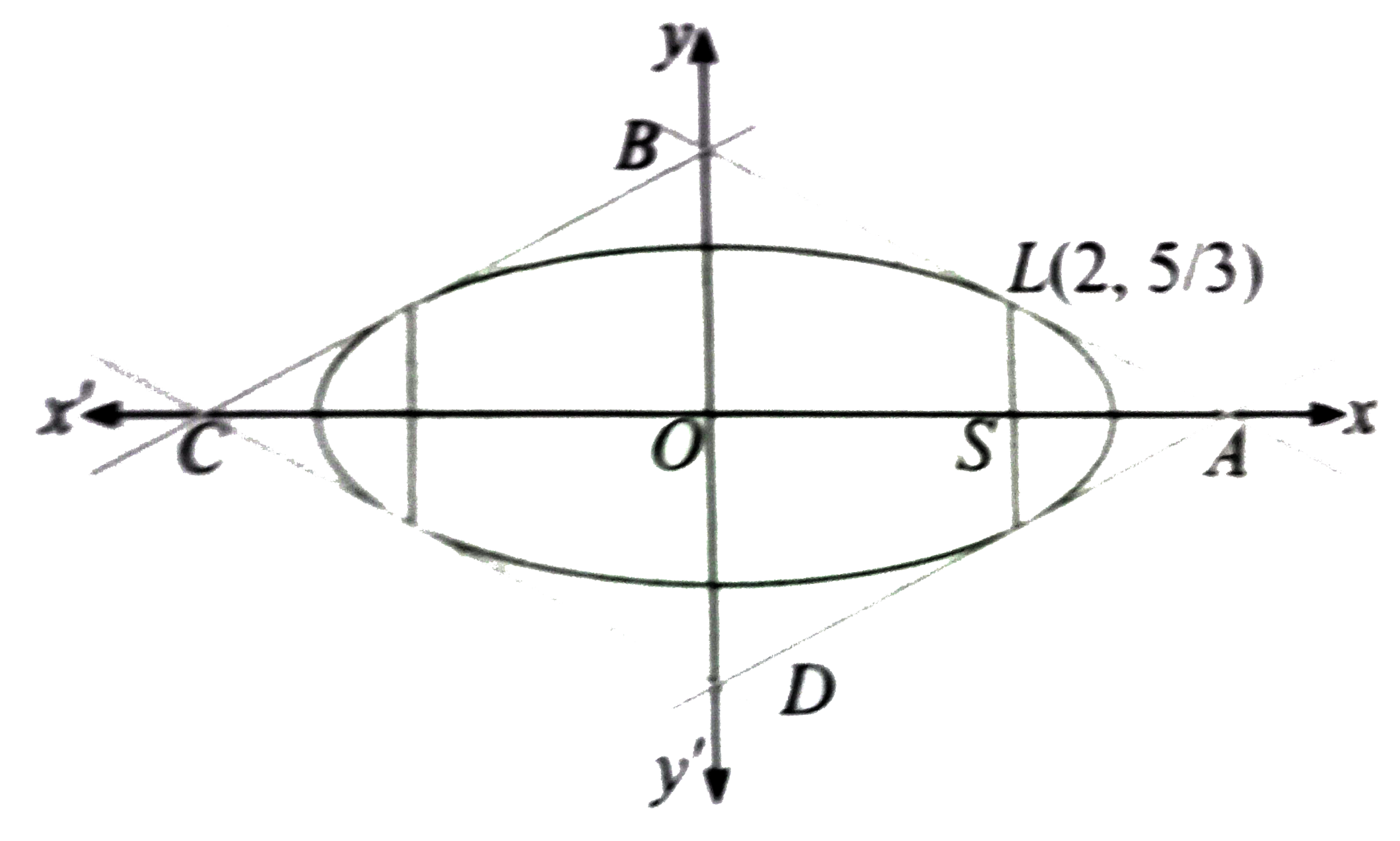
Then a2=9,b2=5. Therefore,
e=√1−59=23 ∴ae=2
Hence, the endpoint of latus rectum in the first quadrant is L(ae,b2/a)≡L(2,5/3)
The equation of tangent at L is 2x9+y3=1
the tangents meets the x-axis at A(9/2,0) and the y-axis at B(0,3). Therefore,
Area of ΔOAPB=12×92×3=274
∴ Area of quadrilateral =4×274=27
Similar Questions
The area (in sq. units) of the quadrilateral formed by the tangents at the end points of the latus rectum to the ellipse x29+y25=1 is (a) 274 (b) 18 (c) 272 (d) 27
View SolutionThe area of the quadrilateral formed by the tangents at the endpoint of the latus rectum to the ellipse x29+y25=1 is (A) 274 sq. unit (B) 9 sq. units (C) 272 sq. unit (D) 27 sq. unit
View Solution
Knowledge Check
The area of the quadrilateral formed by the tangents at the end points of latus rectum of the ellipse 5x2+9y2=45 is
A9B27/2C27/4DNone of theseThe area (in sq. units) bounded by the parabola y=x2−1, the tangent at the point (2,3) to it and the y-axis is
A143B563C83D323
The area (in sq. units) of the triangle formed by the latus rectum and the tangents at the end points of the latus rectum of x216−y29=1 is equal to
View SolutionThe area (in sq. units) of the triangle formed by the latus rectum and the tangents at the end points of the latus rectum of x216−y29=1 is equal to
View SolutionFind the area of parallelogram formed by tangents at the extremities of latera recta of the ellipse x2a2+y2b2=1
View SolutionThe area (in sq. units) bounded by the parabola y=x2−1, the tangent at the point (2,3) to it and the y-axis is
View SolutionThe equations of the tangents drawn at the ends of themajor axis of the ellipse 9x2+5y2−30y=0 are
View Solutionlf a quadrilateral is formed by four tangents to the ellipse x29+y24=1 then the area of the square is equal to
View Solution
