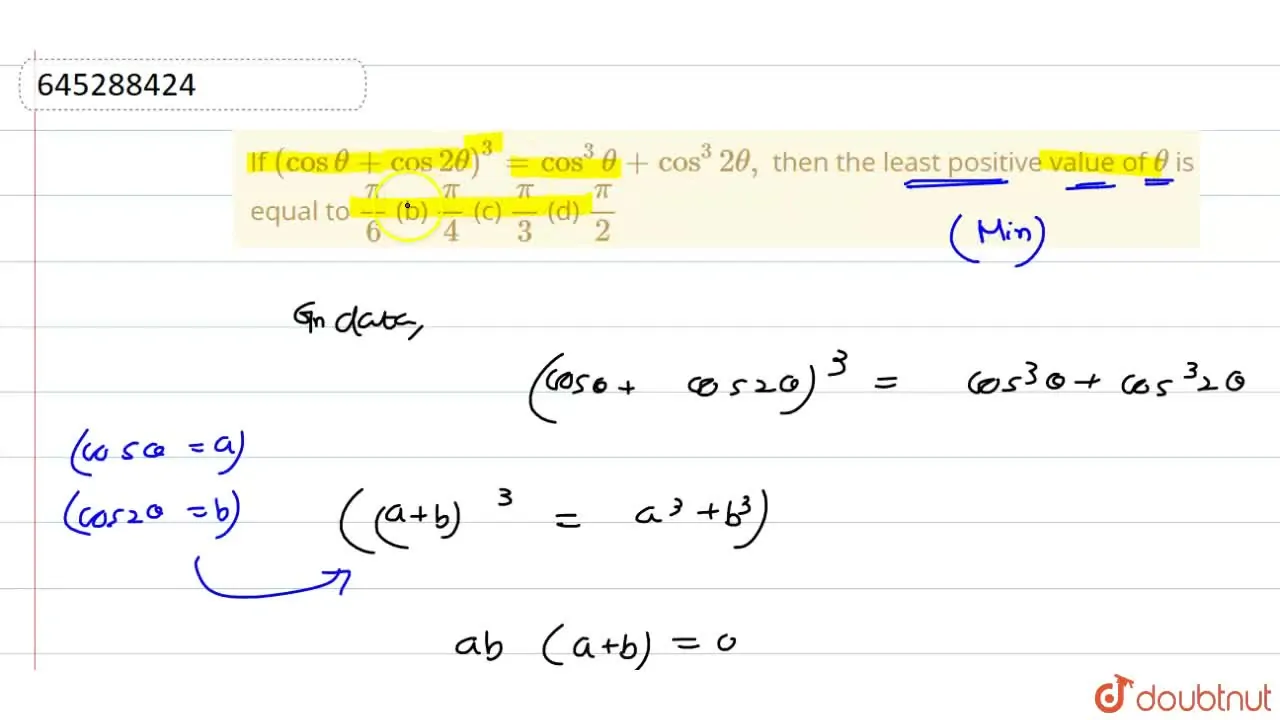
If (cosθ+cos2θ)3=cos3θ+cos32θ, then the least positive value of θ is equal to π6 (b) π4 (c) π3 (d) π2Solution in Tamil
We have (cosθ+cos2θ)3=cos3θ+cos32θ
i.e., (a+b)3=a3+b3
⇒ab(a+b)=0
⇒cosθ=0orcos2θ=0orcosθ+cos2θ=0
⇒θmin=π2orθmin=π4orθmin=π3
⇒θmin=π4
Related Playlists
- BOOK - CENGAGECHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Exercise 4.112videos
TRIGONOMETRIC EQUATIONS
- BOOK - CENGAGECHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Exercise 4.26videos
TRIGONOMETRIC EQUATIONS
- BOOK - CENGAGECHAPTER - TRIGNOMETRIC RATIOS IDENTITIES AND TRIGNOMETRIC EQUATIONSEXERCISE - Question Bank4videos
TRIGNOMETRIC RATIOS IDENTITIES AND TRIGNOMETRIC EQUATIONS
- BOOK - CENGAGECHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - SINGLE CORRECT ANSWER TYPE38videos
TRIGONOMETRIC FUNCTIONS
Similar Questions
Solve sin2θ−cosθ=14,0≤θ≤2π.
01:20View SolutionSolve 2sinθ+1=0.
03:25View SolutionThe number of solution (s) of the equation
√2+cos2x=(sinx+cosx)∈[−π2,π]01:51View SolutionThe circular wire of diameter 10 cm is cut and placed along the circumference of a circle of diameter 1 meter. The angle subtended by the wire at the centre of circle is equal to
08:46View Solutioncos−1(cos(7π6))is equal to (A) 7π6 (B) 5π6 (C) π3 (D) π6
05:09View SolutionGiven both θandϕ are acute angles and sinθ=12,cosφ=13, then the value of θ+φ belongs to (a)(π3,π2] (b) (π2,2π3] (c) (2π3,5π6] (d) (5π6,π]
06:06View SolutionThe value of cos−1√23−cos−1(√6+12√3) is equal to (A) π3 (B) π4 (C) π2 (D) π6
01:58View SolutionIf int_(pi/4)^(pi/3) ((sin^3theta-cos^3theta-cos^2theta)(sintheta+costheta+cos^2theta)^2007)/((sintheta)^2009( costheta)^2009))d theta=((a+sqrtb)^n-(1+sqrtc)^n)/d where a,b,c,d are all positive integers. Find the value of (a+b+c+d).
01:04View SolutionThe value of the determinant |sin theta,cos theta,sin2 thetasin(theta+(2 pi)/(3)),cos(theta+(2 pi)/(3)),sin(2 theta+(4 pi)/(3))sin(theta-(2 pi)/(3)),cos(theta-(2 pi)/(3)),sin(2 theta-(4 pi)/(3))
06:45View SolutionIf 3π2<θ<2π, then the value of sin(3π+θ)−cos(3π2+θ)∣∣∣+cos(3π2−θ)∣∣∣+|sin(3π−θ)|
01:37View SolutionThe smallest positive angle which satisfies the equation 2sin2θ+√3cosθ+1=0 is 5π6 b. 2π3 c. π3 d. π6
06:00View SolutionA value of θ satisfying cosθ+√3sinθ=2 is 5π3 b. 4π3 c. 2π3 d. π3
02:49View SolutionIf (cosθ+cos2θ)3=cos3θ+cos32θ, then the least positive value of θ is equal to π6 (b) π4 (c) π3 (d) π2
03:42View SolutionThe value of theta satisfying the given equation cos theta+sqrt(3)sin theta=2, is (A) (pi)/(3)(B)(5 pi)/(3)(C)(2 pi)/(3) (D) (4 pi)/(3)
02:52View SolutionThe value of cos−1√23−cos−1(√6+12√3) is equal to (A) π3 (B) π4 (C) π2 (D) π6
05:54View SolutionIf (cosθ+cos2θ)3=cos3θ+cos32θ, then the least positive value of θ is equal to π6 (b) π4 (c) π3 (d) π2
06:13View Solution