In a triangle PQR,SandT are points on QRandPR, respectively, such that QS=3SRandPT=4TR. Let M be the point of intersection of PSandQT. Determine the ratio QM:MT using the vector method .Solution in Tamil
The correct Answer is:15:4

Let QM:MT=λ:1andPM:MS=μ:1
and −−→QP=→a,−−→QP=→b
⇒ −−→QT=4→b+→a5
and −−→QM=λλ+1(4→b+→a5) (i)
−−→QS=34→b,−−→QM=μ(34→b)+→aμ+1 (ii)
From (i) and (ii), we have
1μ+1=λ5(λ+1)and4λ5(λ+1)=3μ4(μ+1)
⇒λ=15/4andμ=16/3
∴ QM:MT=15:4
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - INTRODUCTION TO VECTORS EXERCISE - Exercise (Single)34videos
INTRODUCTION TO VECTORS
- BOOK - CENGAGECHAPTER - INTRODUCTION TO VECTORS EXERCISE - Exercise (Multiple)13videos
INTRODUCTION TO VECTORS
- BOOK - CENGAGECHAPTER - INTRODUCTION TO VECTORS EXERCISE - Exercise 1.27videos
INTRODUCTION TO VECTORS
- BOOK - CENGAGECHAPTER - INTEGRALSEXERCISE - Solved Examples And Exercises222videos
INTEGRALS
- BOOK - CENGAGECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - All Questions529videos
INVERSE TRIGONOMETRIC FUNCTIONS
Similar Questions
Four non zero vectors will always be a. linearly dependent b. linearly independent c. either a or b d. none of these
03:01View SolutionThe vectors xˆi+(x+1)ˆj+(x+2)ˆk,(x+3)ˆi+(x+4)ˆj+(x+5)ˆkand(x+6)ˆi+(x+7)ˆj+(x+8)ˆk are coplanar if x is equal to
03:43View SolutionIf →a,→b,→cand→d are four vectors in three-dimensional space with the same initial point and such that 3→a+2→b+→c−2→d=0 , show that terminals A,B,CandD of these vectors are coplanar. Find the point at which ACandBD meet. Find the ratio in which P divides ACandBD.
03:14View SolutionStatement 1: For −1<a<4,∫dxx2+2(a−1)x+a+5 =λlog|g(x)|+c, where λandc are constants Statement 2: For −1<a<4,1x2+2(a−1)x+a+5iscont∈uouunction
02:17View SolutionFind x satisfying [tan−1x]+[cot−1x]=2, where [.] represents the greatest integer function.
View SolutionIn Figure, ∠QPR=∠PQR and M and N are respectively on sides QR and PR of PQR such that QM=PN . Prove that OP=OQ, where O is the point of intersection of PM and QN.
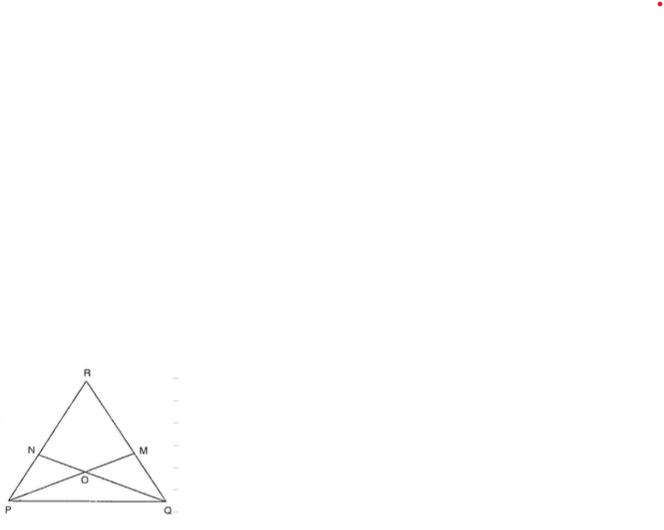 03:47View Solution
03:47View SolutionIn ΔPQR, if PQ=QR and L,M and N are the mid-points of the sides PQ,QR and RP respectively. Prove that LN=MN.
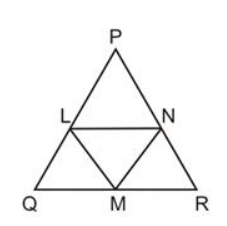 04:01View Solution
04:01View SolutionIn PQR , M and N are points on sides PQ and PR respectively such that PM=15cm and NR=8cm . If PQ=25cm and PR=20cm state whether MNQR .
04:12View SolutionIn Fig. 4.238, S and T are points on the sides PQ and PR respectively of PQR such that PT=2cm , TR=4cm and ST is parallel to QR . Find the ratio of the areas of PST and PQR . (FIGURE)
03:10View SolutionLet A=N×N be the Cartesian product of N and N. Let S={(m,n),(p,q)εA×A:m+q=n+p}
Consider the following statements:
I. If (mn),(p,q))εS and (pqrs)ε then (rsmn)εS
II. There exists at least one element (mnpq)εS such that (pqmn)∉S
Which of the statements given above is /are correct?02:39View SolutionIn a triangle PQR,SandT are points on QRandPR, respectively, such that QS=3SRandPT=4TR. Let M be the point of intersection of PSandQT. Determine the ratio QM:MT using the vector method .
02:37View SolutionIf a−xpx=a−yqy=a−zrandp,q,andr are in A.P., then prove that x,y,z are in H.P.
05:35View SolutionIn Figure, ∠QPR=∠PQR and M and N are respectively on sides QR and PR of PQR such that QM=PN . Prove that OP=OQ, where O is the point of intersection of PM and QN.
05:10View SolutionIn ΔPQR, if PQ=QR and L,M and N are the mid-points of the sides PQ,QR and RP respectively. Prove that LN=MN.
03:09View SolutionIn △PQR , M and N are points on sides PQ and PR respectively such that PM=15cm and NR=8cm . If PQ=25cm and PR=20cm state whether MN∣∣QR .
02:41View SolutionIn Figure, S and T are points on the sides PQ and PR respectively of △PQR such that PT=2cm , TR=4cm and ST is parallel to QR . Find the ratio of the areas of △PST and △PQR .
03:40View Solution

