Suppose that are three non- coplaner in ,Let the components of a vector along be 4,3, and 5, respectively , if the components this vector along are x, y and z , respectively , then the value of is Solution in Tamil
The correct Answer is:9
According to question
(1)
(2)
(3)
Adding (1) and (2), we get
Adding (2) and (3), we get
Adding (1) and (3), we get
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - INTRODUCTION TO VECTORS EXERCISE - Exercise (Numerical)6videos
INTRODUCTION TO VECTORS
- BOOK - CENGAGECHAPTER - INTEGRALSEXERCISE - Solved Examples And Exercises222videos
INTEGRALS
- BOOK - CENGAGECHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - All Questions529videos
INVERSE TRIGONOMETRIC FUNCTIONS
Similar Questions
Let ABC be a triangle whose centroid is G, orhtocentre is H and circumcentre is the origin 'O'. If D is any point in the plane of the triangle such that no three of O, A, C and D are collinear satisfying the relation −−→AD+−−→BD+−−→CH+3−−→HG=λ−−→HD, then what is the value of the scalar 'λ'?
01:45View SolutionStatement 1: For −1<a<4,∫dxx2+2(a−1)x+a+5 =λlog|g(x)|+c, where λandc are constants Statement 2: For −1<a<4,1x2+2(a−1)x+a+5iscont∈uouunction
03:32View SolutionFind x satisfying [tan−1x]+[cot−1x]=2, where [.] represents the greatest integer function.
04:11View SolutionIf vecP+vecQ=vecR and vecP-vecQ=vecS , prove that vecR^2+vecS^2=2(vecP^2+vecQ^2)
04:28View SolutionIf vecP+vecQ=vecR" & "vecR is perpendicular to vecP . define angle between vecP" & "vecQ" if " vec|P|=vec|R|-
View SolutionThree vectors →P,→Q and →R are shown in the figure. Let S be any point on the vector →R. The distance between the points P and S is b∣∣→R∣∣. The general relation among vectors→P,→Q and →S is:
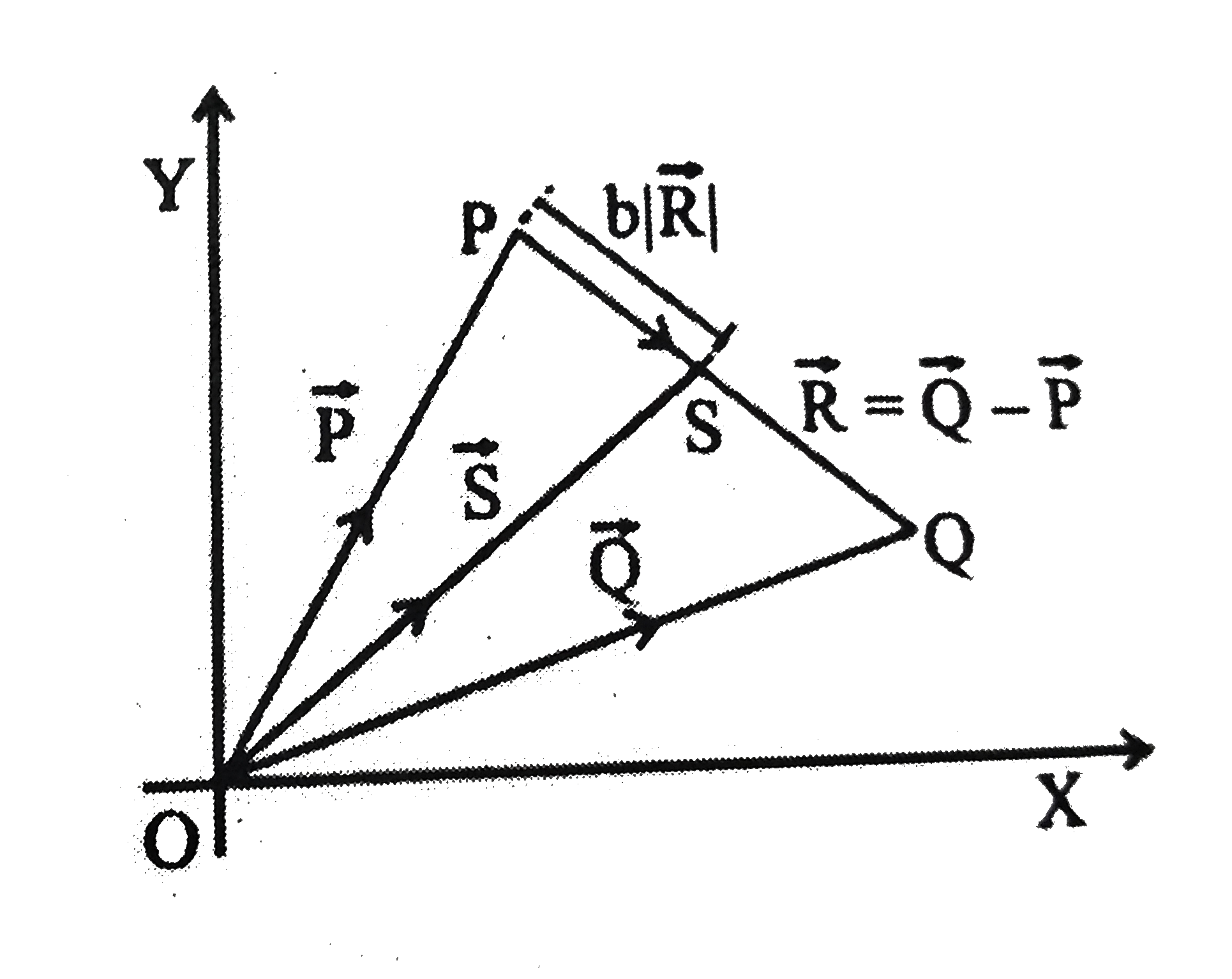 03:27View Solution
03:27View SolutionSuppose that →p,→qand→r are three non- coplaner in R3 ,Let the components of a vector→s along →p,→qand→r be 4,3, and 5, respectively , if the components this vector →s along (−→p+→q+→r),(→p−→q+→r)and(−→p−→q+→r) are x, y and z , respectively , then the value of 2x+y+z is
02:22View SolutionSuppose that →p,→qand→r are three non-coplanar vectors in R3. Let the components of a vectors →s along →p,→qand→r be 4, 3 and 5, respectively. If the components of this vector →s along (−→p+→q+→r),(→p−→q+→r)and(−→p−→q+→r) are x,yandz, respectively, then the value of 2x+y+z is
08:21View SolutionLet →qand→r be non - collinear vectors, If →p is a vector such that →p.(→q+→r)=4and→p×(→q×→r)=(x2−2x+9)→q then +(siny)→r
(x, y) lies on the line14:24View SolutionFor three vectors vecP, vecQ and vecR, vecP+vecQ=vecR and P+Q=R Then prove that vecP and vecQ are parallel to each other.
03:06View SolutionR3 -এর মধ্যে তিনটি অসমতলীয় ভেক্টর হল →p,→q ও→r। মনে করো, →p,→q ও →rভেক্টর তিনটির অভিমুখে →s-ভেক্টরের ভেক্টর উপাংশ 4,3 এবং 5। যদি (−→p+→q+→r),(→p−→q+→r) এবং (−→p−→q+→r) ভেক্টর তিনটির অভিমুখে →s ভেক্টরের ভেক্টর উপাংশ x,y এবং z হয়, তবে 2x+y+z-এর মান নির্ণয় করো।
03:14View SolutionIf →p,→q and →r are perpendicular to →q+→r,→r+→p and →p+→q respectively and if |→p+→q|=6,|→q+→r|=4√3 and |→r+→p|=4 then |→p+→q+→r| is
View Solution→P,→Q,→R,→S are vector of equal magnitude. If →P+→Q−→R=0 angle between →P and →Q is θ1 . If →P+→Q−→S=0 angle between →P and →S is θ2 . The ratio of θ1 to θ2 is
05:56View SolutionSuppose that →p,→qand→r are three non- coplaner in R3 ,Let the components of a vector→s along →p,→qand→r be 4,3, and 5, respectively , if the components this vector →s along (−→p+→q+→r),(→p−→q+→r)and(−→p−→q+→r) are x, y and z , respectively , then the value of 2x+y+z is
02:40View SolutionIf →P+→Q=→Rand P=Q=R√2, then find the angles between the pairs of vectors (→P+→Q),(→Q,→R)and(→R,→P)respectively
03:37View SolutionSuppose that vec p,vecqand vecr are three non- coplaner in R^(3) ,Let the components of a vector vecs along vecp , vec q and vecr be 4,3, and 5, respectively , if the components this vector vec s along (-vecp+vec q +vecr),(vecp-vecq+vecr) and (-vecp-vecq+vecr) are x, y and z , respectively , then the value of 2x+y+z is
02:04View Solution

