A line L1 with direction ratios −3,2,4 passes through the point A(7,6,2) and a line L2 with directions ratios 2,1,3 passes through the point B(5,3,4). A line L3 with direction ratios 2,−2,−1 intersects L1 and L3 at C and D, resectively.
The lenth CD is equal toSolution in Tamil
4
6
9
11
The correct Answer is:C
L1=x−7−3=y−62=z−24 and L2=x−52=y−31=z−43
∴D(2μ+5,μ+3,3μ+4)
So, 2−3λ−2μ2=3+2λ−μ−2=−2+4λ−3μ−1
∴λ=2,μ=1
So, C(1,10,10) and D(7,4,7) ⇒ CD=9.
Topper's Solved these Questions
Similar Questions
The ratio in which the plane 2x−1=0 divides the line joining (−2,4,7) and (3,−5,8) is
View SolutionLet A(0,6,6), B(6,6,0) and C(6,0,6) are three points and point D is moving on the line x+z−3=0=y. If G is centroid of ΔABC, then minimum value of GD is
View SolutionLine L1 is parallel to vector →α=−3ˆi+2ˆj+4ˆk and passes through a point A(7,6,2) and line L2 is parallel vector →β=2ˆi+ˆj+3ˆk and point B(5,3,4). Now a line L3 parallel to a vector →r=2ˆi−2ˆj−ˆk intersects the lines L1andL2 at points CandD, respectively, then find ∣∣→CD∣∣.
View SolutionIn the xy plane,the line L_(1) passes through the point (1,1) and the line L_(2) passes through the point (-1,1). If the difference of the slopes of the lines is 2. Then the locus of the point of intersection of the lines L_(1) and L_(2) is
View SolutionThe line l_(1) passing through the point (1,1) and the l_(2), passes through the point (-1,1) If the difference of the slope of lines is 2. Find the locus of the point of intersection of the l_(1) and l_(2)
View SolutionIf lines l1,l2 and l3 pass through a point P, then they are called…………. Lines.
View SolutionA line L1 with direction ratios −3,2,4 passes through the point A(7,6,2) and a line L2 with directions ratios 2,1,3 passes through the point B(5,3,4). A line L3 with direction ratios 2,−2,−1 intersects L1 and L3 at C and D, resectively.
The lenth CD is equal to
View SolutionA line L1 with direction ratios −3,2,4 passes through the point A(7,6,2) and a line L2 with directions ratios 2,1,3 passes through the point B(5,3,4). A line L3 with direction ratios 2,−2,−1 intersects L1 and L3 at C and D, resectively. The equation of the plane parallel to line L1 and containing line L2 is equal to
View SolutionA line L1 with direction ratios −3,2,4 passes through the point A(7,6,2) and a line L2 with directions ratios 2,1,3 passes through the point B(5,3,4). A line L3 with direction ratios 2,−2,−1 intersects L1 and L3 at C and D, resectively.
The volume of parallelopiped formed by −−→AB,−−→AC and −−→AD is equal to
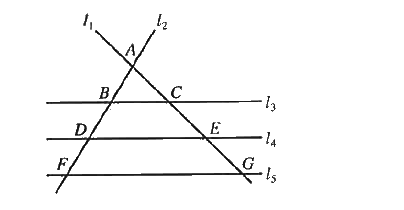
View SolutionLines l2andl2 intersect each other and 3 parallel lines, l3,l4andl5, at the points shown in the figure below. The ratio of the perimeter of △ABC to the perimeter of △AFG is 1:3 . The ratio of DE to FG is 2:3. What is the ratio of AC to CE?
View SolutionEquation of a line passing through the point (2,−3,2) and equally inclined to the Line L1andL2 may be equal to :
View SolutionLine L1 is parallel to vector →α=−3ˆi+2ˆj+4ˆk and passes through a point A(7, 6, 2) and line L2 is parallel to a vector →β=2ˆi+2ˆj+3ˆk and passes through a point B(5,3,4). Now a line L3 parallel to a vector →r=2ˆi−2ˆj−ˆk intersects the line L1 and L2 at point C and D respectively, Find ∣∣∣−−→CD∣∣∣.
View SolutionIf the direction ratios of the lines L1andL2 are 2, -1, 1 and 3, -3, 4 respectively, then the direction cosines of a line that is perpendicular to both L1andL2 are
View SolutionL1 is a line passing through the point A(n,n+1) having slope, n,L2 is a line passing through the point B(−n,n2) and is perpendicular to L1, If L1 and L2 intersect on y-axis, then n is equal to ________ (n>0)
View SolutionA line L1 with direction ratios −3,2,4 passes through the point A(7,6,2) and a line L2 with directions ratios 2,1,3 passes through the point B(5,3,4). A line L3 with direction ratios 2,−2,−1 intersects L1 and L2 at C and D, resectively.
The lenth CD is equal to
View SolutionA line L1 with direction ratios −3,2,4 passes through the point A(7,6,2) and a line L2 with directions ratios 2,1,3 passes through the point B(5,3,4). A line L3 with direction ratios 2,−2,−1 intersects L1 and L3 at C and D, resectively. The equation of the plane parallel to line L1 and containing line L2 is equal to
View Solution
