The range of a for which the equation x2+ax−4=0 has its smaller root in the interval (−1,2) is

A

(−∞,−3)

B

(0, 3)

C

(0,∞)

D

(−∞,−3)∪(0,∞)

Text Solution
Verified by Experts

The correct Answer is:A

Clearly , f(−1)>0,f(2)<0
Now ,
f(0)=−4<0
⇒f(−1)=1−a−4>0
and f(2)=4+2a−4<0
⇒a<−3anda<0
⇒a∈(−∞),−3)
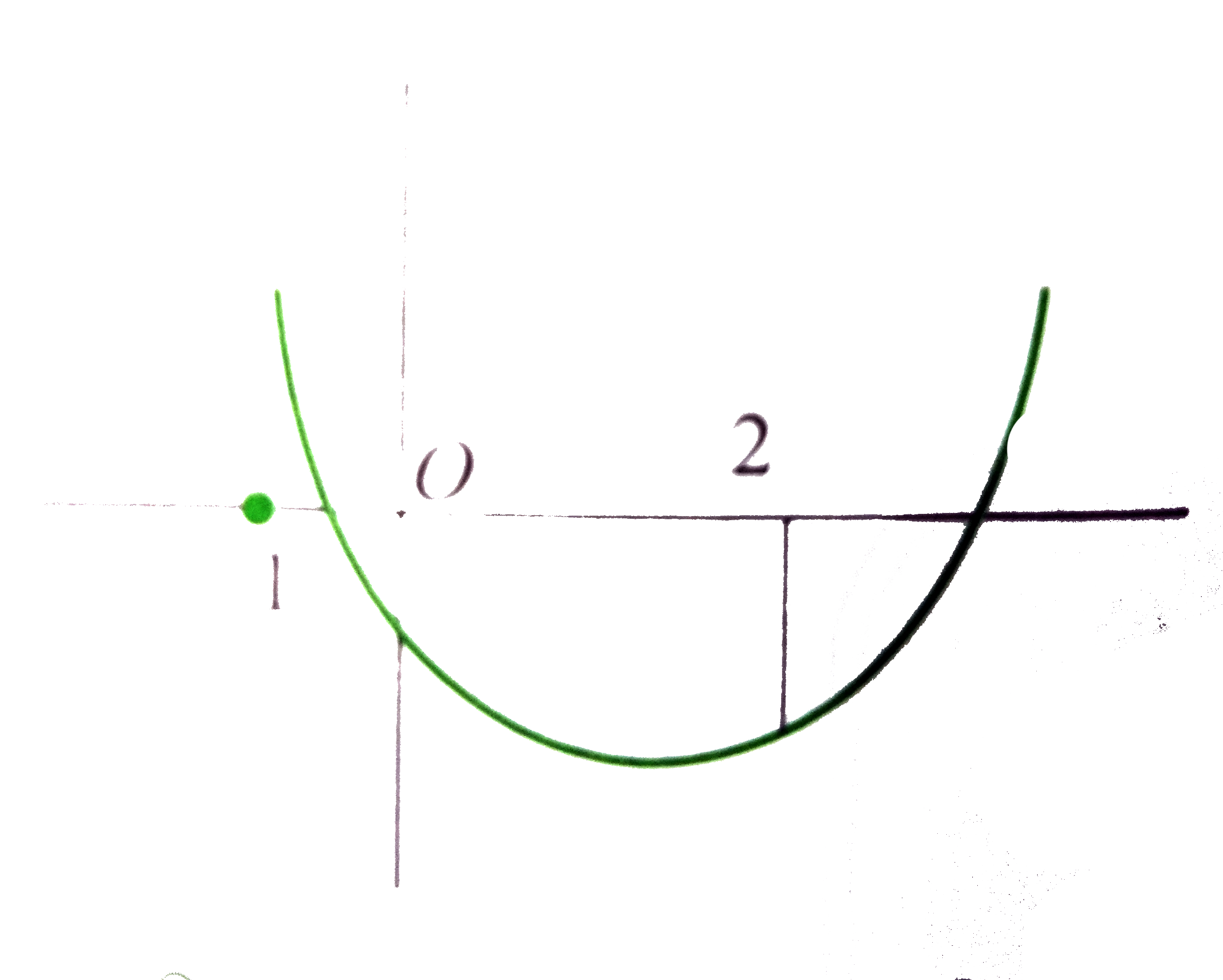
ocr_image

Updated on:21/07/2023
Doubtnut Promotions Banner
|
Class 12MATHSQUADRATIC EQUATIONS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • The value of 'a' for which the equation ax2−2√5x+4=0 has equal roots ,is

    A54
    B45
    C−54
    D−53

  • The number of values of k for which the equation x2−2x+k=0 has two distinct roots lying in the interval (0,1) is

    A0
    B1
    C2
    Dinfinitely many

  • The value of 'a' for which the equation ax2−2√5x+4=0 has equal roots ,is

    A54
    B45
    C−54
    D−53