The range of the function tan−1(x2+1x2+√3),x∈R is a.[π6,π2) b. [π6,π3) c. [π6,π4] d. none of theseSolution in Tamil
[π6,π2)
[π6,π3)
[π6,π4)
none of these
The correct Answer is:C
We have
f(x)=tan−1(x2+1x2+√3),x∈R
Let y=x2+1x2+√3
⇒ yx2+√3y=x2+1
⇒ (√3y−1)=(1−y)x2
∴ x2=(√3y−11−y)≥0
So, √3y−1y−1≤0
⇒ y∈[1√3,1)
∴ Range of f(x)=[π6,π4)
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - FUNCTIONSEXERCISE - Multiple Correct Answers Type10videos
FUNCTIONS
- BOOK - CENGAGECHAPTER - FUNCTIONSEXERCISE - Comprehension Type7videos
FUNCTIONS
- BOOK - CENGAGECHAPTER - EQUATION OF PLANE AND ITS APPLICATIONS -IIEXERCISE - DPP 3.418videos
EQUATION OF PLANE AND ITS APPLICATIONS -II
- BOOK - CENGAGECHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - Exercise18videos
GETTING STARTED WITH GRAPHS
Similar Questions
The function f(x)=cos−1⎛⎝2[|sinx|+|cosx|]sin2x+2sinx+114⎞⎠ is defined if x belongs to (where [.] represents the greatest integer function)
03:15View SolutionLet f(x)=x2−2x−1∀x∈R Let f:(−∞,a]→[b,∞), where a is the largest real number for which f(x) is bijective. If f:R→R , g(x)=f(x)+3x−1 , then the least value of function y=g(|x|) is
04:14View SolutionLet A(0,6,6), B(6,6,0) and C(6,0,6) are three points and point D is moving on the line x+z−3=0=y. If G is centroid of ΔABC, then minimum value of GD is
03:49View SolutionDoes the following graph pass the vertical or horizontal line test ?
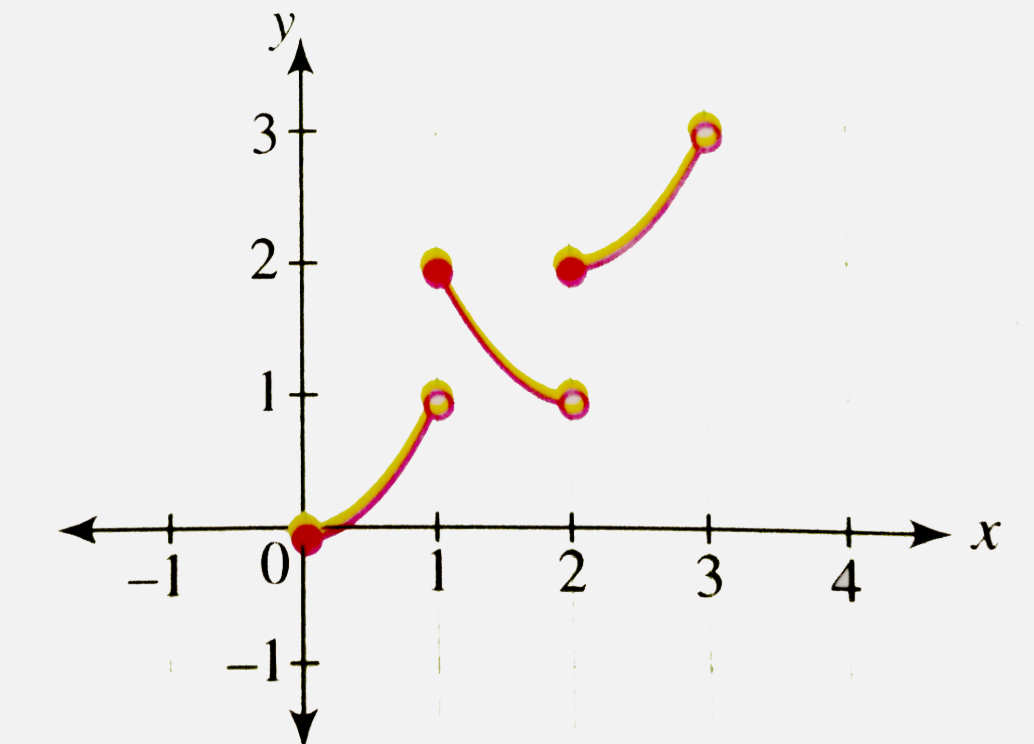 01:19View Solution
01:19View SolutionThe range of f(x)=sin−1(x2+1x2+2) is [0,π2] (b) (0,π6) (c) [π6,π2] (d) none of these
01:18View SolutionThe range of f(x)=sin−1(√x2+x+1)is (0,π2) (b) (0,π3) (c) (π3,π2) (d) [π6,π3]
01:56View SolutionThe range of the function tan−1(x2+1x2+√3),x∈R is [π6,π2) b. [π6,π3) c. [π6,π4] d. none of these
04:45View SolutionIf tan−1(cotθ)=2 θ , then θ= ±π3 (b) ±π4 (c) ±π6 (d) none of these
06:56View Solution∫√3111+x2dx is equal to π12 b. π4 c. π6 d. π3
06:33View Solutionsin−1(−12)+tan−1(√3)= (A) −π6 (B) π3 (C) π6 (D) none of these
03:17View SolutionThe range of f(x)=sin−1(x2+1x2+2) is (a)[0,π2] (b) (0,π6) (c) [π6,π2] (d) none of these
04:59View SolutionRange of the function f(x)=√cos−1(√log4x)−π2+sin−1(1+x24x) is equal to (A) (0,π2+√π2] (B) [π2,π2+√π2] (C) [π6,π4) (D) {π6}
02:59View SolutionThe range of the function tan−1(x2+1x2+√3),x∈R is a.[π6,π2) b. [π6,π3) c. [π6,π4] d. none of these
01:26View SolutionThe range of f(x)=sin−1(x2+1x2+2) is (a)[0,π2] (b) (0,π6) (c) [π6,π2] (d) none of these
03:24View SolutionRange of the function f(x)=√cos−1(√log4x)−π2+sin−1(1+x24x) is equal to
(A) (0,π2+√π2]
(B) [π2,π2+√π2]
(C) [π6,π4)
(D) {π6}04:00View SolutionIf tan−1(cotθ)=2 θ , then θ= (a) ±π3 (b) ±π4 (c) ±π6 (d) none of these
03:22View Solution

