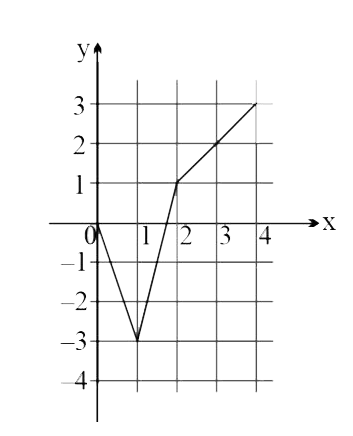
A continuous, even periodic function f with period 8 is such that f(0)=0,f(1)=−2,f(2)=1,f(3)=2,f(4)=3, then the value of tan−1tan{f(−5)+f(20)+cos−1(f(−10))+f(17)} is equal toSolution in Tamil
2π−3
3−2π
2π+3
3−π
The correct Answer is:D
f(−5)=f(3)=2,f(20)=f(4)=3,f(−10)=f(−2)=f(2)=1,
f(17)=f(1)=−2
∴ tan−1tan{f(−5)+f(20)+cos−1(f(−10))+f(17)}
=tan−1tan(2+3+0−2)=3−π.
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - FUNCTIONSEXERCISE - Multiple Correct Answers Type10videos
FUNCTIONS
- BOOK - CENGAGECHAPTER - FUNCTIONSEXERCISE - Comprehension Type7videos
FUNCTIONS
- BOOK - CENGAGECHAPTER - EQUATION OF PLANE AND ITS APPLICATIONS -IIEXERCISE - DPP 3.418videos
EQUATION OF PLANE AND ITS APPLICATIONS -II
- BOOK - CENGAGECHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - Exercise18videos
GETTING STARTED WITH GRAPHS
Similar Questions
The function f(x)=cos−1⎛⎝2[|sinx|+|cosx|]sin2x+2sinx+114⎞⎠ is defined if x belongs to (where [.] represents the greatest integer function)
04:13View SolutionLet f(x)=x2−2x−1∀x∈R Let f:(−∞,a]→[b,∞), where a is the largest real number for which f(x) is bijective. If f:R→R , g(x)=f(x)+3x−1 , then the least value of function y=g(|x|) is
03:09View SolutionLet A(0,6,6), B(6,6,0) and C(6,0,6) are three points and point D is moving on the line x+z−3=0=y. If G is centroid of ΔABC, then minimum value of GD is
03:13View SolutionDoes the following graph pass the vertical or horizontal line test ?
 05:40View Solution
05:40View SolutionLet f(x)=tan^(-1)((1)/(2)tan2x)+tan^(-1)(cot x)+tan^(-1)(cot^(3)x)then (1) f((3 pi)/(8))=pi(2)f((pi)/(8))=0(3)f((pi)/(8))=pi(4)f((3 pi)/(8))=0
03:43View SolutionIf f is continuous function in [1,2] such that |f(1)+3|<|f(1)|+3 and |f(2)+10|=|f(2)|+10,(f(2)≠0) then the
03:23View SolutionGiven is a partial graph of an even periodic function f whose period is 8. If[*] denotes greatest integer function then find the value of the expression. f(-3) + 2/(-1)|+[f(7/8)]+f(0)+arccos(f(-2))+f(-7)+f(20)
03:11View SolutionLet f(x) be a cubic polynomial on R which increases in the interval (-oo,0)uu(1,oo) and decreases in the interval (0,1). If f'(2)=6 and f(2)=2, then the value of tan^(-1)(f(1))+tan^(-1)(f((3)/(2)))+tan^(-1)(f(0)) equals
02:36View SolutionA continuous,even periodic function f with period 8 is such that f(0)quad =0.f(1)=2.f(2)=1f(3)=2.f(4)=3 then the value of cos^(-1)(cos(f(9)+2f(20))) is equal to
08:11View SolutionLet f(x) is a continuous function such that f(-1) = -2,f(0) = -1,f(1) = 0,f (2) = 1, f(3) = 0,f (4) = -1 and f(5) = 1 then minimum number of roots of f'(x) + xf " (x) = 0 in the interval (-1,5) are
07:05View SolutionA continuous, even periodic function f with period 8 is such that f(0)=0,f(1)=−2,f(2)=1,f(3)=2,f(4)=3, then the value of tan−1tan{f(−5)+f(20)+cos−1(f(−10))+f(17)} is equal to
05:54View SolutionA function f is such that f(x+1)=f(x)+f(1)+1 for all real values of x. Find f(0) If it is given that f(1)=1, find f(2),f(3)andf(−1).
03:18View SolutionA function f is said to be periodic if it repeats its nature after certain interval and that interval is called period of the function. If T be the period of f(x), then f(x + T) = f(x). For example f(x) = tan x is periodic with period π. Then find the period of f(x) that satisfies the following condition.
(i) f(x + 1) - f(x + 3) = 0
(ii) f(x + 3) + f(x) = 0
(iii) f(x-1) + f(x+3) = f(x+1) + f(x + 5)
(iv) f(x+p)=1+{(1−f(x−p))2n+1}12n+1,n∈N05:06View SolutionIf f(x) is a quadratic function and f(2) = 1, f(3) = 6 and f(-1) = 10, find f(x) and show that, f(1) = 0.
02:40View SolutionGiven below is a partial graph of an even periodic function f whose period is 8. If [*] denotes greatest integer function then find the value of the expression.
f(−3)+2|f(−1)|+[f(78)]+f(0)+arccos(f(−2))+f(−7)+f(20)
 04:51View Solution
04:51View SolutionIf f'(x)=1−2sin2xf(x),(f(x)≥0,∀ξnRandf(0)=1) then f(x) is a periodic function with the period
11:49View Solution

