Let f(x)=x1+x and let g(x)=rx1−x , Let S be the set off all real numbers r such that f(g(x))=g(f(x)) for infinitely many real number x. The number of elements in set S isSolution in Tamil
1
2
3
5
The correct Answer is:B
f(g(x))=rx1+(r−1),g(f(x))=rx.
If f(g(x))=g(g(x))
⇒ rx1+(r−1)x=rx
⇒ rx[1−11+(r−1)x]=0
If this is to ture for infinitely many (all) x, then r = 0 or r-1 = 0
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - FUNCTIONSEXERCISE - Multiple Correct Answers Type10videos
FUNCTIONS
- BOOK - CENGAGECHAPTER - FUNCTIONSEXERCISE - Comprehension Type7videos
FUNCTIONS
- BOOK - CENGAGECHAPTER - EQUATION OF PLANE AND ITS APPLICATIONS -IIEXERCISE - DPP 3.418videos
EQUATION OF PLANE AND ITS APPLICATIONS -II
- BOOK - CENGAGECHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - Exercise18videos
GETTING STARTED WITH GRAPHS
Similar Questions
The function f(x)=cos−1⎛⎝2[|sinx|+|cosx|]sin2x+2sinx+114⎞⎠ is defined if x belongs to (where [.] represents the greatest integer function)
01:32View SolutionLet f(x)=x2−2x−1∀x∈R Let f:(−∞,a]→[b,∞), where a is the largest real number for which f(x) is bijective. If f:R→R , g(x)=f(x)+3x−1 , then the least value of function y=g(|x|) is
02:18View SolutionLet A(0,6,6), B(6,6,0) and C(6,0,6) are three points and point D is moving on the line x+z−3=0=y. If G is centroid of ΔABC, then minimum value of GD is
03:00View SolutionDoes the following graph pass the vertical or horizontal line test ?
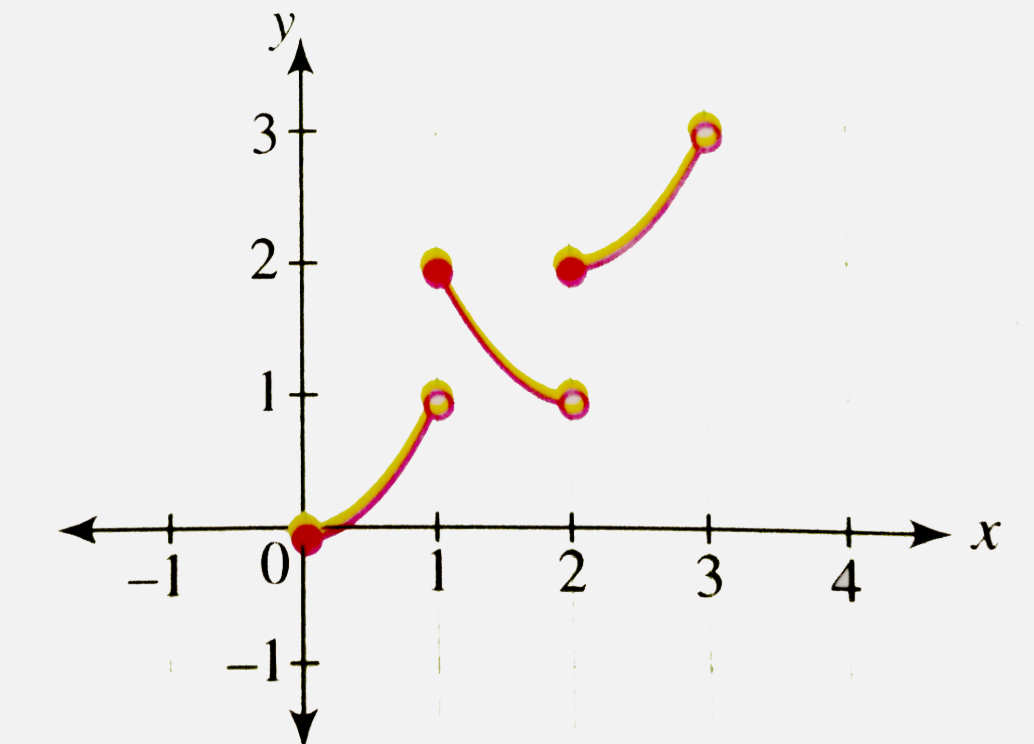 02:34View Solution
02:34View Solutionlet f(x) =√x and g(x) =x be function defined over the set of non negative real numbers . find (f+g)(x),(fg)(x)and(fg)(x) .
03:04View SolutionLet f(x)=√xand g(x)=xbe two functions defined over the set of nonnegative real numbers. Find (f+g)(x), (fg)(x), (fg)(x)and (fg)(x).
01:27View SolutionLEt f(x)=2^(100)x+1 and g(x)=3^(100)x+1 Then the set of real numbers x such that f(g(x))=x is
02:56View SolutionLet F and G be two real-valued function defined on R (the set of all real numbers)
F(x)={|x+1|x{:(,xle0,),(,xgt0,):}G(x)={:{(,|x|+1,),(,-|x-2,):}x≤1x>1 and H(x)=F(x)+G(x).
Point of discontinuity of H(x) are01:51View SolutionLet R be the set of real numbers . If the function f:R→Randg:R→R be defined by f(x)=4x+1 and g(x)=x2+3, then find (go f ) and (fo g) .
02:02View SolutionLet f(x)=√xandg(x)=x be two functions defined over the set of non-negative real numbers. Find (f+g)(x),(f−g),(fg)(x)and(fg)(x).
02:21View SolutionLet f(x)=√xandg(x)=x be two functions defined over the set of non-negative real numbers. Find (f+g)(x),(f−g),(fg)(x)and(fg)(x).
01:44View SolutionLet f(x)=√xandg(x)=x be two functions defined over the set of non-negative real numbers. Find (f+g)(x),(f−g),(fg)(x)and(fg)(x).
02:56View SolutionLet f(x)=√xandg(x)=x be two functions defined over the set of non-negative real numbers. Find (f+g)(x),(f−g),(fg)(x)and(fg)(x).
06:20View Solutionlet f(x) =√x and g(x) =x be function defined over the set of non negative real numbers . find (f+g)(x) , (f-g)(x) , (fg)(x) and (f/g)(x) .
04:03View SolutionLet f(x)=√x and g(x)=x be two functions defined over the set of nonnegative real numbers. Find (f+g)(x), (f−g)(x), (fg)(x) and (fg)(x).
02:13View SolutionLet f(x)=√xand g(x)=xbe two functions defined over the set of nonnegative real numbers. Find (f+g)(x), (fg)(x), (fg)(x)and (fg)(x).
02:11View Solution

