A regular square based pyramid is inscribed in a sphere of given radius R so that all vertices of the pyramid belong to the sphere. Find the greatest value of the volume of the pyramid.Solution in Tamil
The correct Answer is:6481r3
If we cut the sphere from the center along the diagonal of the square base we get the view show in figure

Let r be the radius of the spere Then
Height of the pyramid =r+r cosθ
Diagonal of the square base =2rsinθ
∴ side of the squre base =2rsinθ√2
Let v be the volume of the pyaramid .Then
V=13 (Area of the base xx Height)
=132rsinθ(√2)2×(r+rcosθ)
∴dVdθ=23r3[sin2θ(1+cosθ)−sin3θ]
=23r3[2sin2θcos2θ−sin3θ]
=23r3×sinθ(2cosθ+2cos2θ−sin2θ)
=23r3sinθ(3cos2θ+2cosθ−1)
=23r3sinθ(cosθ+1)(3cosθ−1)
For maximum or minimum values of v we must have dVdθ=0
or 3cosθ−1=0
cos θ=13
Hence V is maximum when cos θ=13andsinθ=2√23
The maximum value of V is given by
V=23r3×89(1+13)=6481r3
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Exercise (Single)93videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGECHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Exercise (Multiple)40videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGECHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Exercise 6.69videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGECHAPTER - METHODS OF DIFFERETIATIONEXERCISE - Question Bank13videos
METHODS OF DIFFERETIATION
- BOOK - CENGAGECHAPTER - MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSEXERCISE - Comprehension Type6videos
MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONS
Similar Questions
A function is matched below against an interval where it is supposed to be increasing. Which of the following parts is incorrectly matched? Interval, Function (a)[2, ∞) , 2x3−3x2−12x+6 (b)(−∞,∞) , x3=3x2+3x+3 (c)(−∞−4) , x3+6x2+6 (d)(−∞,13) , 3x2−2x+1
05:52View SolutionLet f(x)=⎧⎪ ⎪⎨⎪ ⎪⎩x2+3x,−1≤x<0−sinx,0≤x<π/2−1−cosx,π2≤x≤π . Draw the graph of the function and find the following
(a) Range of the function
(b) Point of inflection
(c) Point of local minima02:12View SolutionA private telephone company serving a small community makes a profit of Rs. 12.00 per subscriber, if it has 725 subscribers. It decides to reduce the rate by a fixed sum for each subscriber over 725, thereby reducing the profit by 1 paise per subscriber. Thus, there will be profit of Rs. 11.99 on each of the 726 subscribers, Rs. 11.98 on each of the 727 subscribers, etc. What is the number of subscribers which will give the company the maximum profit?
02:12View SolutionLet f:(−5,5)→R be a differentiable function with f(4) = 1, f′(4)=1,f(0)=−1 and f^(')(0) = 1,Ifg(x) = f(2f^(2)(x)+2))^(2),then - g^(')(0) equals
02:27View SolutionLet f:R→R,y=f(x),f(0)=0,f'(x)>0andf''(x)>0. Three point A(α,f(α)),B(β,f(β)),C(γ,f(γ))ony=f(x) such that 0<α<β<γ.
Which of the following is false ?03:40View SolutionA regular square based pyramid is inscribed in a sphere of given radius R so that all vertices of the pyramid belong to the sphere. Find the greatest value of the volume of the pyramid.
02:25View SolutionRegular pyramid a pyramid is said to be a regular pyramid if its base is a regular figure i.e. all sides of its base are equal.
02:22View SolutionRegular pyramid a pyramid is said to be a regular pyramid if its base is a regular figure.
04:14View Solutionकिसी पिरामिड का आधार 40 सेमी. भुजा वाला वर्ग है। यदि किसी पिरामिड का आयतन 800cm3 है। पिरामिड की ऊंचाई ज्ञात करें?
02:16View SolutionThe base of a right pyramid is an equilateral triangle of perimeter 8 dm and the height of the pyramid is 30√3 cm. Find the volume of the pyramid.
03:21View Solution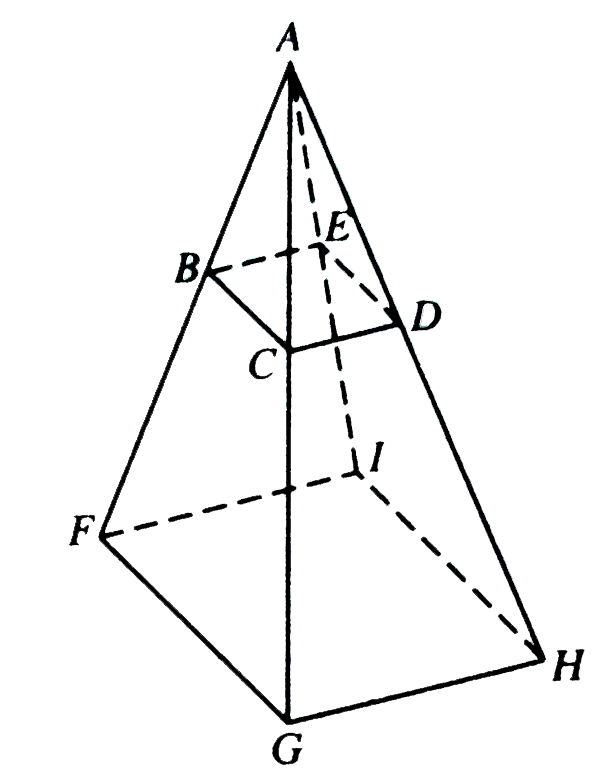
The pyramid in the figure above has square base FGHI , and all triangular faces are congruent. The base BCDE of the small pyramid is also square , and is parallel to FGHI. If the ratio of the area of square BCDE to the area of square FGHI is 1:4 , what is the ratio of the volume of the small pyramid to the volume of the large pyramid ?01:12View SolutionThe base of a pyramid is a square whose side is 10 cm. It's slant and vertical heights are 13 and 12 . Then , find the total surface area and volume of the pyramid .
04:14View SolutionThere is a pyramid on a base which is a regular hexagon of side 2a. If every slant edge of this pyramid is of length (5a)2 then the volume of this pyramid must be :
02:14View SolutionA regular square pyramid is 3m Height and the perimeter of its base is 16 m. Find the volume of the pyramid.
05:55View SolutionThe lateral edge of a regular rectangular pyramid is acmlong. The lateral edge makes an angle α with the plane of the base. Find the value of α for which the volume of the pyramid is greatest.
02:02View SolutionThe base of a square pyramid is a square.
01:55View Solution

