Which of the following is true about point of extremum x=a of function y=f(x)?
At x =a, function y = f(x) may be discontinous
At x =a function y = f(x) may be continous but non differentiable
At x =a function y= f(x) may have point of inflection
none of these
The correct Answer is:1,2,3
The following function is discontinous at x =2 but has point of maxima

f(x)=|x| has point of minima at x=0 thought it is non differetiable at x=0

In the following figure y=f(x) has point of inflection at x=0 as curve changed its concavity at x=0 howere x=0 is point of minima for the fucntion

Topper's Solved these Questions
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBOOK - CENGAGECHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Exercise (Comprehension)
42 Videos
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBOOK - CENGAGECHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Linked comprehension type
8 Videos
- MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSBOOK - CENGAGECHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Exercise (Single)
93 Videos
- METHODS OF DIFFERETIATIONBOOK - CENGAGECHAPTER - METHODS OF DIFFERETIATIONEXERCISE - Question Bank
13 Videos
- MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSBOOK - CENGAGECHAPTER - MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSEXERCISE - Comprehension Type
6 Videos
Similar Questions
Knowledge Check
which of the folloiwng function has point of extremum at x =0?
Af(x) =e−|x|Bf(x) = sin |x|Cf(x)={x2+4x+3x<0−xx≥0Df(x)={x2+4x+3x<0−xx≥0Which one of the following is true about the polynomial function y=−7x5+3x3−18x2−7x+23?
Ay→+∞, whenx→−∞By→−∞, whenx→−∞Cy→+∞, whenx→+∞Dnone of the abovey = f(x) which has differential equation y(2xy+ex)dx−exdy=0 passing through the point (0,n 1). Then which of the following is/are true about the function?
Ax=1+√2 is point of local maximaBx=1−√2 is point of local minimaClimx→∞f(x)=−∞Dlimx→−∞f(x)=0
The graph of the function y=f(x). Then which of the following curve represent the graph of the function y=|f(x)|
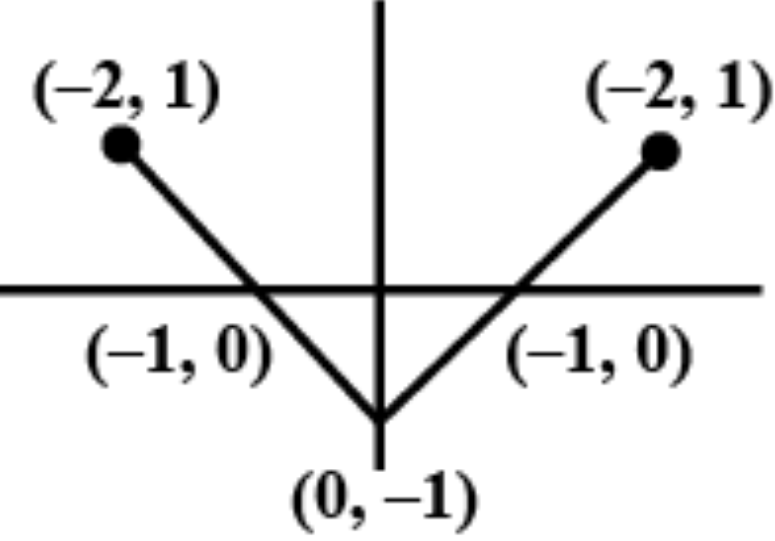
View SolutionWhich of the following statements about the function y=f(x) graphed here are true, an which are false ? limx→2f(x)=2
View SolutionThe number of points of extremum of the function f(x)=(x−2)23(2x+1) is
View Solutiony = f(x) which has differential equation y(2xy+ex)dx−exdy=0 passing through the point (0,1). Then which of the following is/are true about the function?
View SolutionWhich of the following hold(s) good for the function f(x)=2x−3x23? (a)f(x) has two points of extremum. (b)f(x) is convave upward ∀x∈R. (c)f(x) is non-differentiable function. (d)f(x) is continuous function.
View Solution
