consider the graph of y=g(x)=f'(x) given that f(c ) =0, where y=f(x) is a polynomial funtion

The function y = f(x),a≤x≤b,has
exactly one local maxima
one local minima and one maxima
exactly one local minima
none of these
The correct Answer is:4
As f(x) is a decreasing function for all x in (a,b),f(x) has no local mixima or minima.
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Matrix Match Type12videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGECHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Exercise (Numerical)20videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGECHAPTER - MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONSEXERCISE - Exercise (Comprehension)42videos
MONOTONICITY AND MAXIMA MINIMA OF FUNCTIONS
- BOOK - CENGAGECHAPTER - METHODS OF DIFFERETIATIONEXERCISE - Question Bank13videos
METHODS OF DIFFERETIATION
- BOOK - CENGAGECHAPTER - MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONSEXERCISE - Comprehension Type6videos
MONOTONOCITY AND NAXINA-MINIMA OF FUNCTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
The graph of y=f(x) is given below
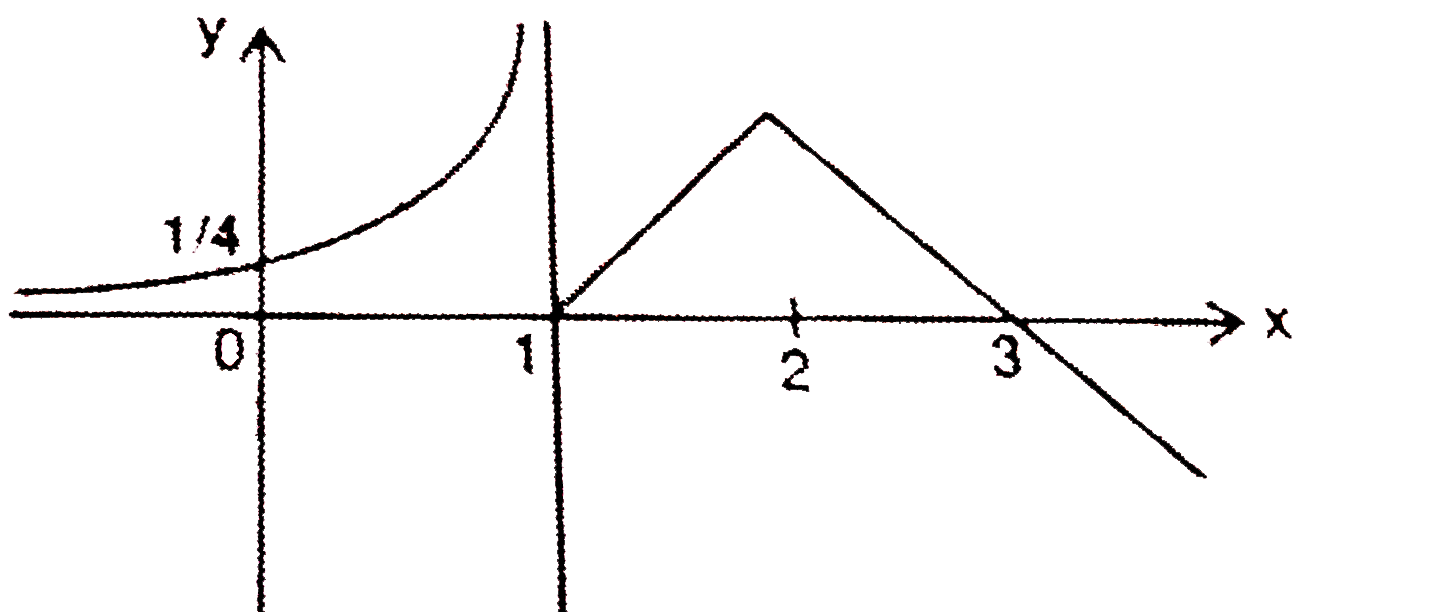
then the graph y=|f(|x|)| is :A B
B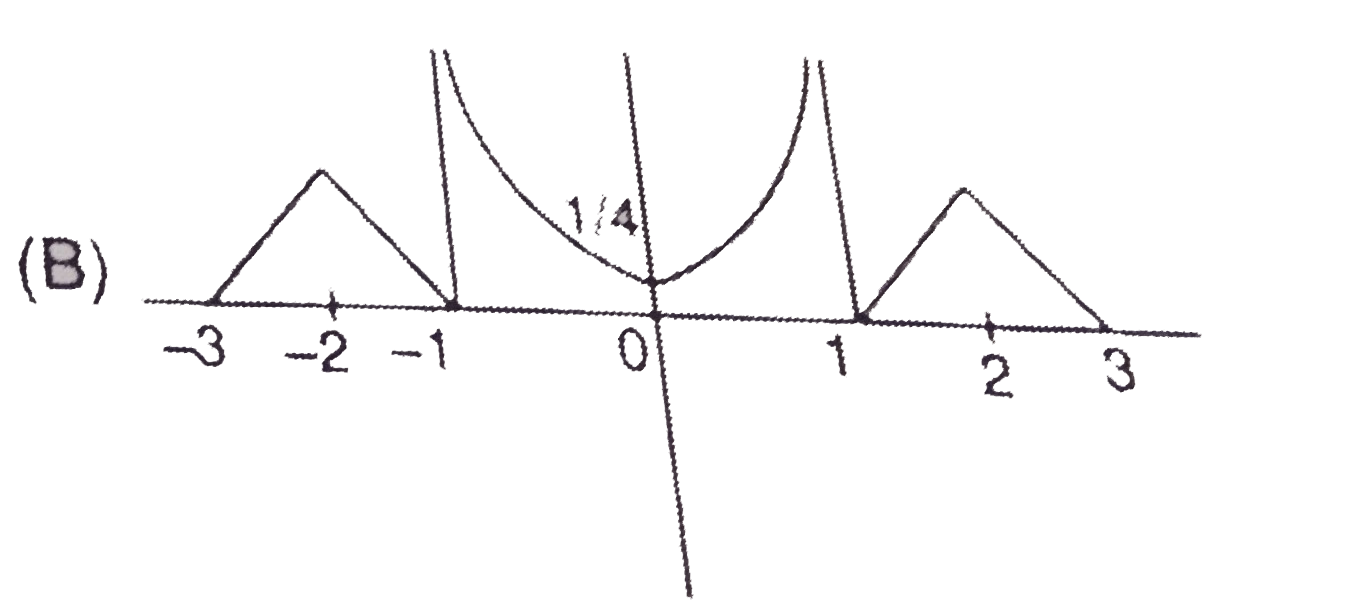 C
C Dnone of these
Dnone of these
If the function / satisfies the relation f(x+y)+f(x−y)=2f(x),f(y)∀x,y∈Randf(0)≠0 , then f(x)isa≠venfunction f(x)isanoddfunction Iff(2)=a,thenf(−2)=a Iff(4)=b,thenf(−4)=−b
View SolutionSolve: dydx+y⋅f'(x)=f(x)⋅f'(x), where f(x) is a given function.
View SolutionProve that f(x)givenbyf(x+y)=f(x)+f(y)∀x∈R is an odd function.
View Solution(2x+3y5)+2f(x)+3f(y)5 and f′(0)=p and f(0)=q. Then f(0) is.
(where f(x) is a polynomial function)View SolutionFind the area of the region bounded by y=f(x),y=|g(x)| and the lines x=0,x=2, where f,g are continuous function satisfying f(x+y)=f(x)+f(y)−8xy,∀x,y∈R and g(x+y)=g(x)+g(y)+3xy(x+y),∀x,y∈R also , f'(0)=8andg'(0)=−4.
View SolutionFind the area of the region bounded by the curves y=f(x),y=|g(x)| and lines x=0,x=2, where f and g are continuous functions satisfying f(x+y)=f(x)+f(y)−8xy for all x,y∈R and g(x+y)=g(x)+g(y)+3xy(x+y) for all x,y∈R. Also f'(0)=8 and g\'(0)=-4.
View SolutionGiven the graph of y=f(x).
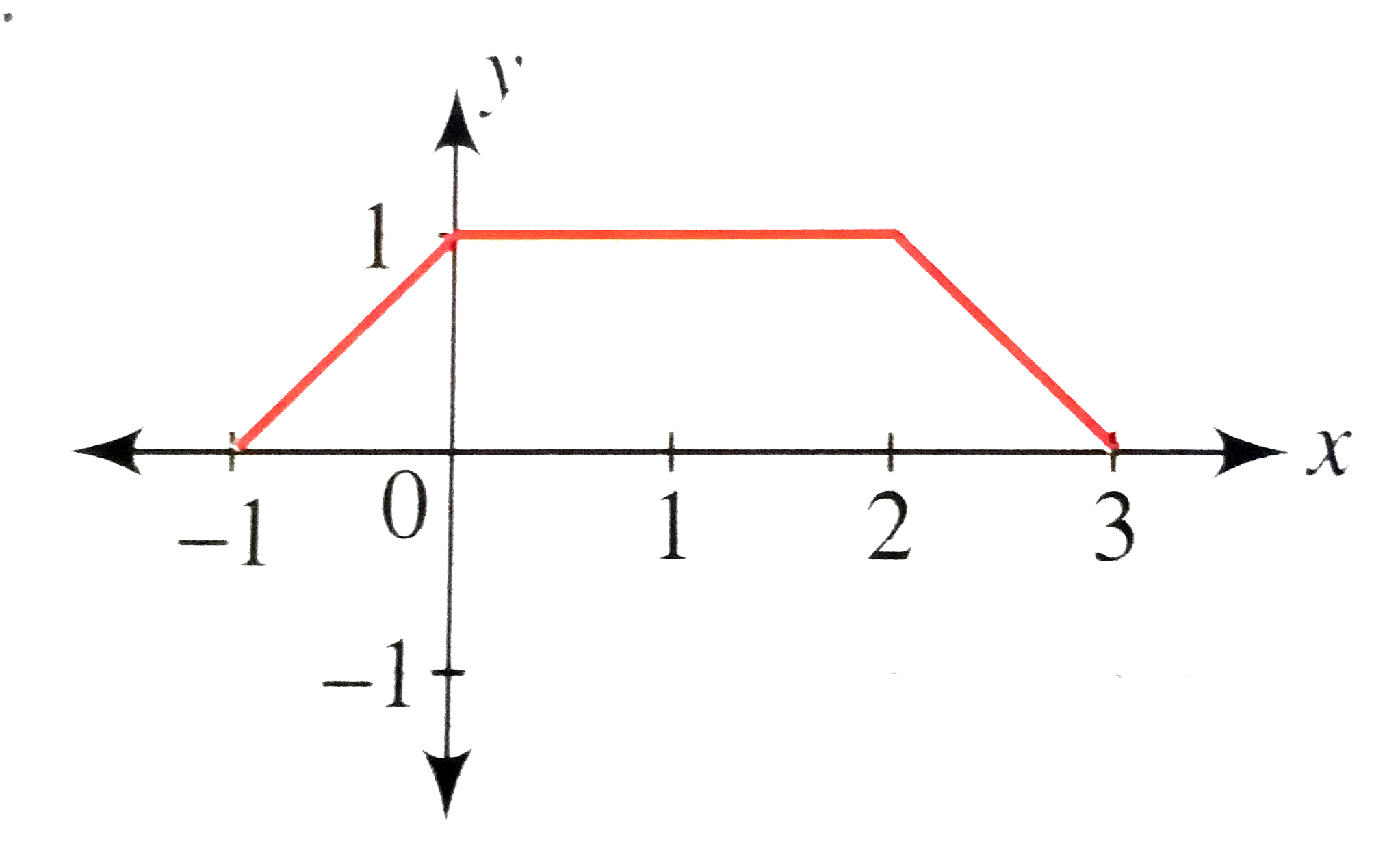
Draw the graphs of the followin.
(a) y=f(1−x) (b) y=−2f(x)
(c) y=f(2x) (d) y=1−f(x)View Solution

