Let the quadratic equation (c−5)x2−2cx+c−4=0 has one root in (0,2) and other root in (2,3) then find the number of intergral values of c in solution set (a) 18 (b) 12 (c) 11 (d) 10Solution in Tamil
11
10
12
18
The correct Answer is:A
Let f(x)=(c−5)x2−2cx+(c−4)=0.
Then, according to problem, the graph of g=f(x) will be either of the two ways, show below.
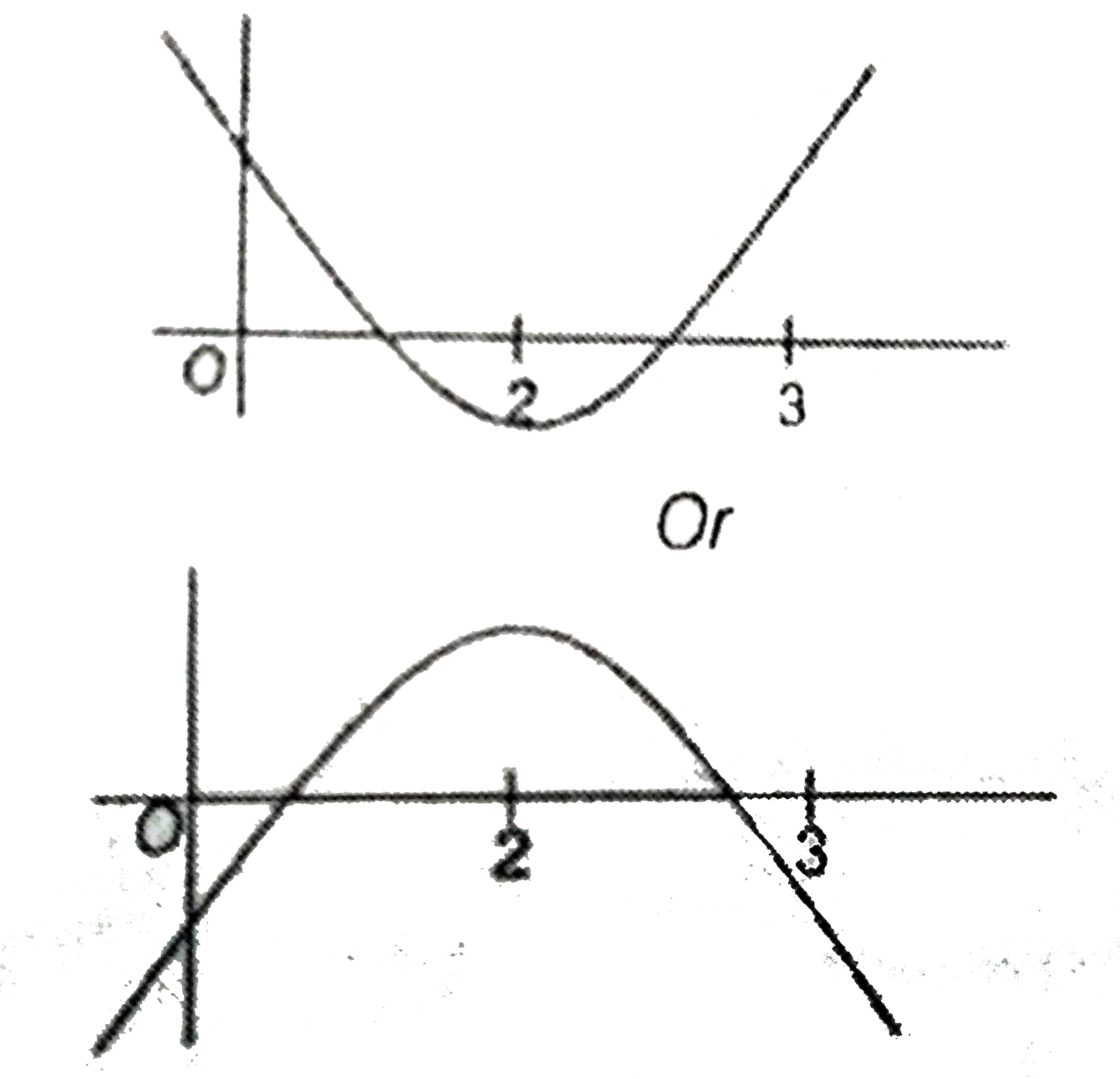
In both cases f(0).f(2)<0andf(2)f(3)<0
Now, consider f(0)f92)<0
⇒(c−4)[4(c−5)−4c+(c−4)]<0
⇒(c−4)(c−24)<0
⇒c∈(4,24) ...(i)

Similiarly, f(2).f(3)<0
⇒[4(c−5)−4c+(c−4)]
[9(c−5)−6c+(c−4)]<0
⇒(c−24)(4c−49)<0

⇒c∈(494,24) ...(ii)
From Eqs. (i) and (ii), we get
c∈(494,24)
∴ Integral vaues of c are 13,14 ....., 23, Thus, 11 integral values of c are possible.
Similar Questions
If the roots of the equaion x4−12x3+cx2+dx+81=0 are positive then the value of c is The value of d is. Roots of the equation 2cx+d=0 is
06:55View SolutionIf the roots of the equaion x4−12x3+cx2+dx+81=0 are positive then the value of c is The value of d is. Roots of the equation 2cx+d=0 is
06:55View SolutionLet a,b,c,d be distinct real numbers and a and b are the roots of the quadratic equation x2−2cx−5d=0 . If c and d are the roots of the quadratic equation x2−2ax−5b=0 then find the numerical value of a+b+c+d.
04:38View SolutionLet a,b and be the roots of the equation x2−10xc−11d=0 and those roots of c and d of x2−10ax−11b=0,. then find the value of a+b+c+d
04:42View SolutionLet a,b,c,d be distinct real numbers and a and b are the roots of the quadratic equation x2−2cx−5d=0 . If c and d are the roots of the quadratic equation x2−2ax−5b=0 then find the numerical value of a+b+c+d
06:26View SolutionConsider the quadratic equation (c - 5)x^(2) - 2cx + (c - 4) = 0, c ne 5 . Let S be the set of all integral values of c for which one root of the equation lies in the interval (0, 2) and its other root lies in the interval (2, 3). Then the number of elements in S is a. 11 b. 18 c. 10 d. 12
03:43View SolutionLet a,b,c,d be distinct real numbers and a and b are the roots of the quadratic equation x2−2cx−5d=0 . If c and d are the roots of the quadratic equation x2−2ax−5b=0 then find the numerical value of a+b+c+d.
05:05View Solution

