If the roots of the equation $x^{2} - 2 a x + a^{2} - a - 3 = 0$ are real and less than 3, then Solution in Tamil

A

$a < 2$

B

$2 \leq a \leq 3$

C

$3 < a \leq 4$

D

$a > 4$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Let $f (x) = x^{2} - 2 a x + a^{2} + a - 3$
Since, both root are less than 3.
$\Rightarrow a < 3, β < 3$
$\Rightarrow S u m, S = α + β < 6$
$\Rightarrow \frac{α + β}{2} < 3$
$\Rightarrow \frac{2 a}{2} < 3$
$\Rightarrow a < 3 ... (i)$
Again, product, $P = α β$
$\Rightarrow P < 9 \Rightarrow α β < 9$
$\Rightarrow a^{2} + a - 3 < 9$
$\Rightarrow a^{2} + a - 12 < 0$
$\Rightarrow (a - 3) (a + 4) < 0$
$\Rightarrow - 4 < a < 2 . . (i i)$
Again, $D = B^{2} - 4 A C \geq 0$

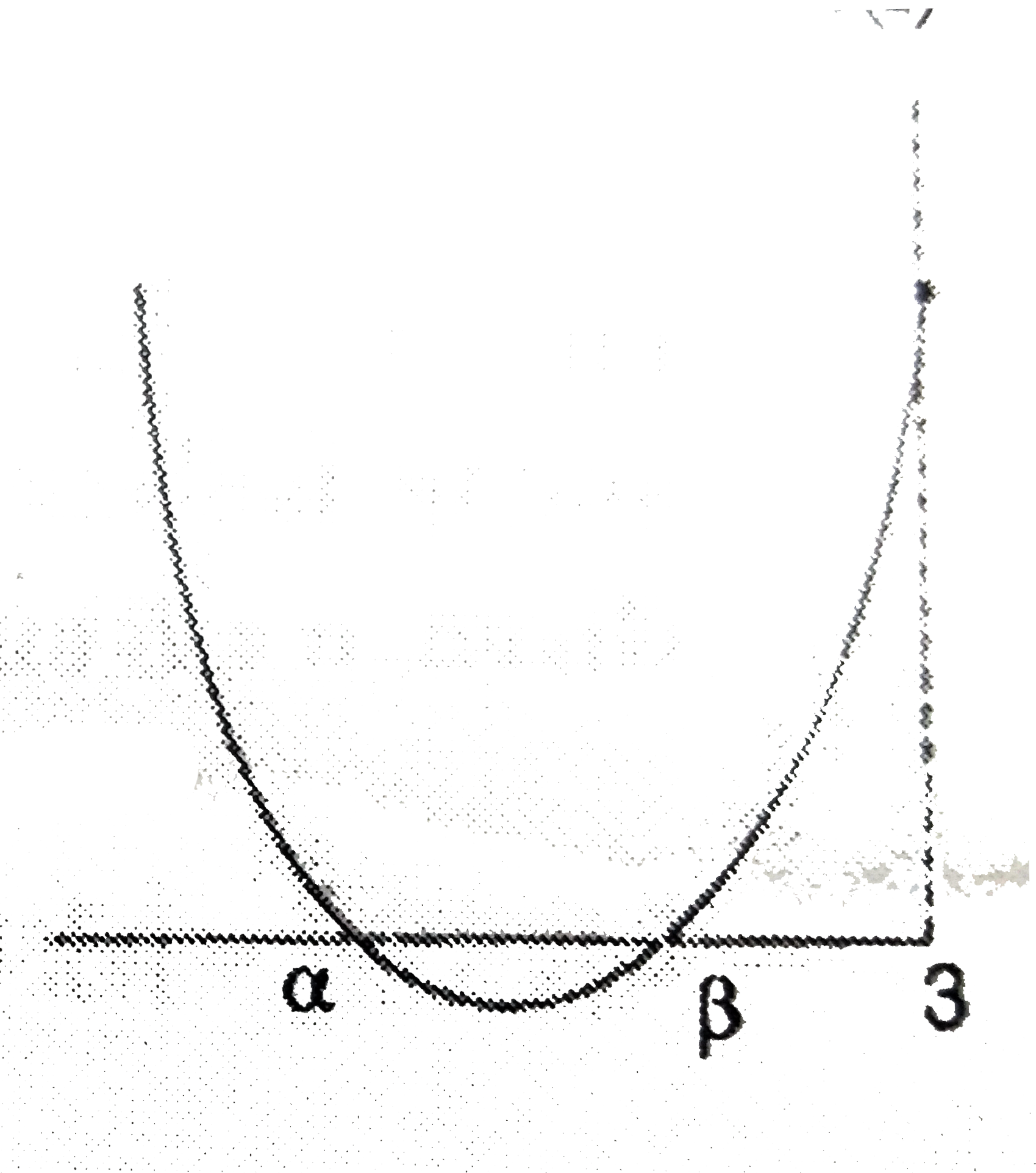
$\Rightarrow {(- 2 a)}^{2} - 4.1 (a^{2} + a - 3) \geq 0$
$\Rightarrow 4 a^{2} - 4 a^{2} - 4 a + 12 \geq 0$
$\Rightarrow - 4 a + 12 \geq 0 \Rightarrow a \leq 3 ... (i i i)$
Again, $= a f (3) > 0$
$\Rightarrow 1 . [{(3)}^{2} - 2 a (3) + a^{2} + a - 3] > 0$
$\Rightarrow 9 - 6 a + a^{2} + a - 3 > 0$
$\Rightarrow a^{2} - 5 a + 6 > 0$
$\Rightarrow (a - 2) (a - 3) > 0$
$∴ a \in (- \infty, 2) \cup ? (2, \infty) ... (i v)$
From Eqs. (i),(ii),(iii), and (iv), we get $a \in (- 4, 2) .$
Note There is correction in answer $< 2 should be - 4 < a < 2 .$

Updated on:21/07/2023

|

Class 12 MATHS QUADRATIC EQUATIONS

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile