Question

The angle of elevation of the top of a vertical tower standing on a horizontal plane is observed to be ${45}^{\circ }$ from a point A on the plane. Let B be the point 30 m vertically above the point A. If the angle of elevation of the top of the tower from B be ${30}^{\circ }$, then the distance then the distance (in m) of the foot of the tower from the point A is

Options

A. `15 (3+sqrt(3))`
B. `15 (5-sqrt(3))`
C. `15 (3-sqrt(3))`
D. `15 (1+sqrt(3))`

Answer

A

Explanation

According to the question, we have the following figure.

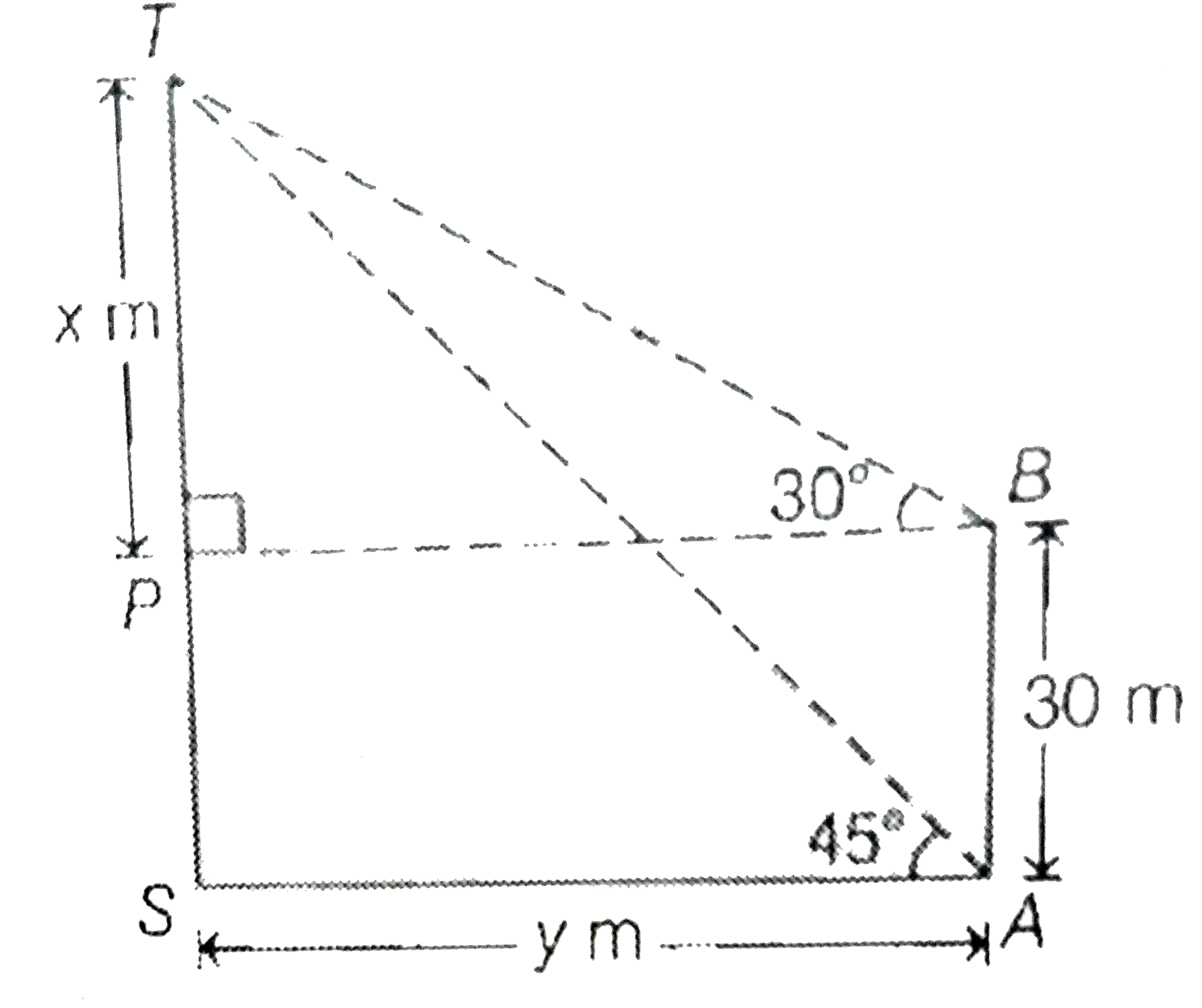
Now, let distance of foot of the tower from the point A is y m.
Draw `BP_|_ ST` such that PT - x m.
Then, in `DeltaTPB`, we have
`tan 30^(@) = (x)/(y)`
`implies x = (1)/(sqrt(3))y " ...(i)"`
and in `DeltaTSA`, we have `tan45^(@)=(x+30)/(y)`
`implies y = x + 30 " ...(ii)"`
On the elimination of quantity x from Eqs. (i) and (ii), we get
`y = (1)/(sqrt(3))y+30`
`implies y(1-(1)/(sqrt(3))=30)`
`implies y=(30sqrt(3))/(sqrt(3)-1)=(30sqrt(3)(sqrt(3)+1))/(3-1)`
`=(30)/(2)sqrt(3)(sqrt(3)+1)=15(3+sqrt(3))`