Question

ABC is a triangular park with AB = AC = 100 m. A vertical tower is situated at the mid-point of BC. If the angles of elevation of the top of the tower at A and B are ${\cot }^{-1}\left(3\sqrt{2}\right)$ and $\cos e{c}^{-1}\left(2\sqrt{2}\right)$ respectively, then the height of the tower (in m) is

Options

A. 25
B. 20
C. `10sqrt(5)`
D. `(100)/(3sqrt(3))`

Answer

B

Explanation

Given ABC is a triangular park with AB = AC = 100 m. A vertical tower is situated at the mid-point of BC.
Let the height of the tower is h m.
Now, according to given information, we have the following figure.

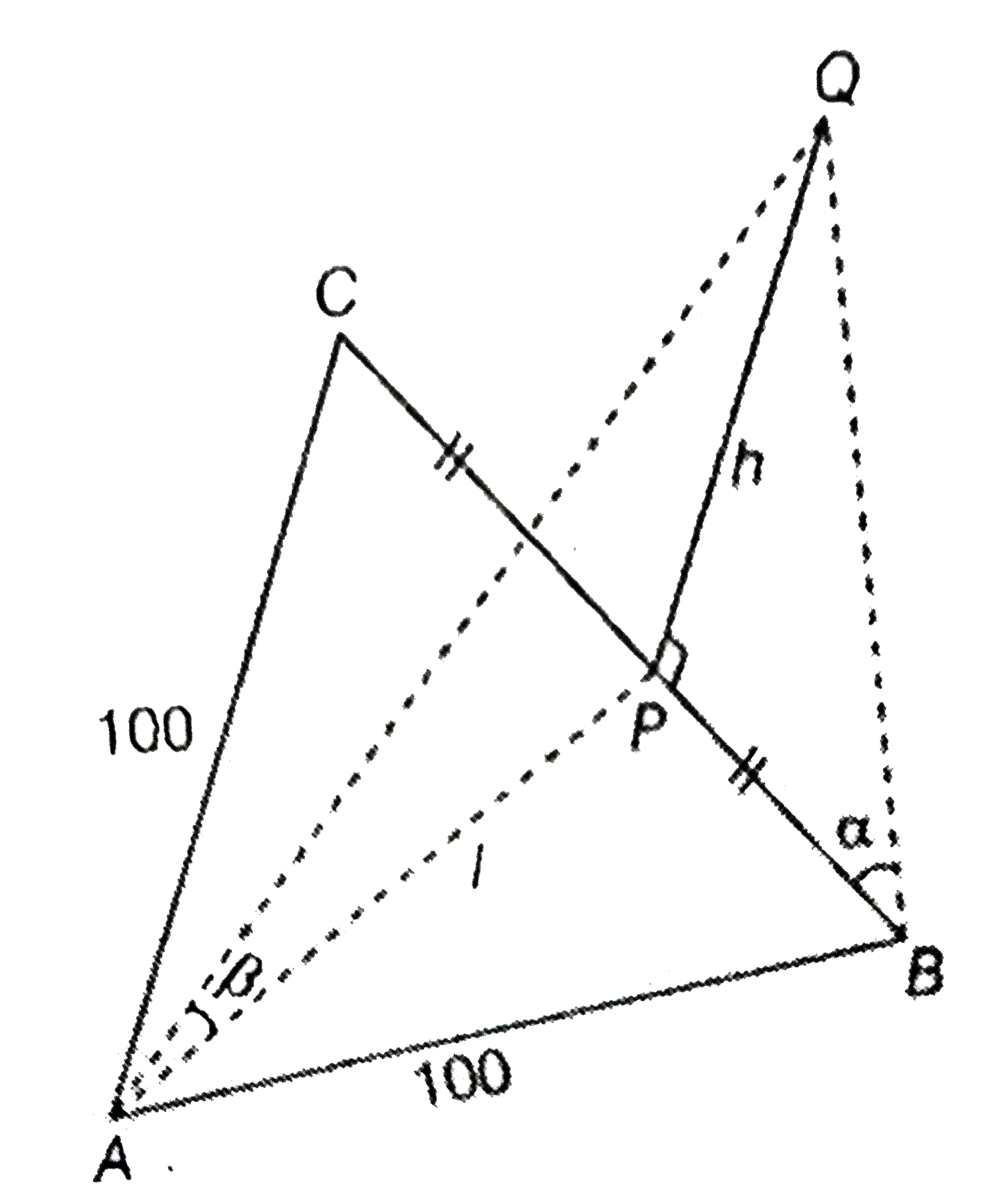
From the figure and given information, we have
`beta=cot^(-1)(3sqrt(2))`
and `alpha=cosec^(-1)(2sqrt(2))`
Now, in `DeltaQPA`,
`cotbeta = (l)/(h)`
`implies l=(3sqrt(2))h" ...(i)"`
and in `DeltaBPQ, tan alpha = (h)/(BP)`
`implies cot alpha=(BP)/(h)=(sqrt((100^(2))-l^(2)))/(h)`
`[because " p is mid-point of isosceles "DeltaABC, AP _|_ BC]`
`implies h^(2)cot^(2)alpha=(100)^(2)-l^(2)`
`impliesh^(2)(cosec^(2)alpha-1)=(100)^(2)-(3sqrt(2)h)^(2)" [from Eq. (i)]"`
`implies h^(2)(8-1)=(100)^(2)-18h^(2)`
`implies 25h^(2)=(100)^(2)`
`implies h^(2)=((100)/(5))^(2)implies h = 20 m`