Question

Let ${\displaystyle i={\int }_a^b(x^4-2x^2)dx}$ for ${\displaystyle (a,b)}$ which given integration is minimum ${\displaystyle (b>0)}$ (a) ${\displaystyle (\sqrt{2},-\sqrt{2})}$ (b) ${\displaystyle (0,\sqrt{2})}$ (c) ${\displaystyle (-\sqrt{2},\sqrt{2})}$ (d) ${\displaystyle (\sqrt{2},0)}$

Options

A. `(-sqrt(2),0)`
B. `(0,sqrt(2))`
C. `(sqrt(2),-sqrt(2))`
D. `(-sqrt(2),sqrt(2))`

Answer

D

Explanation

We have , I `=int_(a)^(b)(x^(4)-2x^(2))dx`
Let `f(x)=x^(4)-2x^(2)=x^(2)(x^(2)-2)`
` =x^(2)(x-sqrt(2))(x+sqrt(2))`
Graph ` y=f(x)=x^(4)-2x^(2)` is

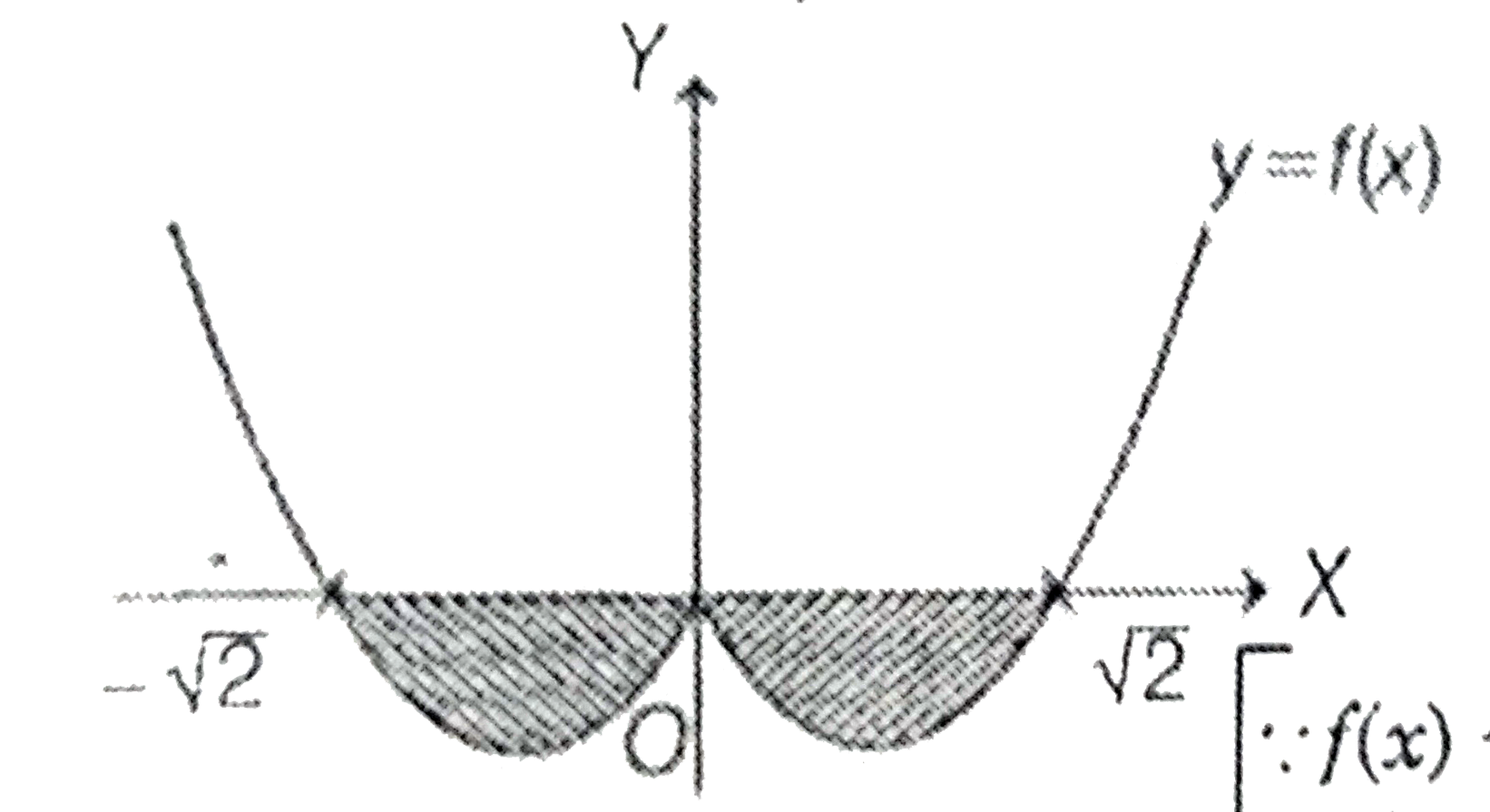
Note that the definite integral `int_(a)^(b)(x^(4)-2x^(2)) dx` represent the area bounded by ` y= f(x),x =` a , b and the X - axis.
But between `x=-sqrt(2)andx=sqrt(2),f(x)` lies below the X - axis and so value definite integral will be negative. Also , as long as f(x) lie below the X - axis , the value of definite integral will be minimum.
`:.(a.b)=(-sqrt(2),sqrt(2)` for minimum of I.