Radioactive disintegration is a first order reaction and its rate depends only upon the nature of nucleus and does not depend upon external factors like temperature and pressure. The rate of radioactive disintegration (Activity) is represented as
−dNdt=λN Where λ= decay constant, N= number of nuclei at time t, N0 =initial no. of nuclei. The above equation after integration can be represented as
λ=2.303tlog(N0N)
Half-life period of U is 2.5×105 years. In how much time will the amount of U237 remaining be only 25% of the original amount ?
a) 2.5×105 year
b) 1.25×105 years
c) 5×105 years
d) none of these Solution in Punjabi
2.5×105 year
1.25×105 years
5×105 years
none of these
The correct Answer is:C
Step by step video & image solution for Radioactive disintegration is a first order reaction and its rate depends only upon the nature of nucleus and does not depend upon external factors like temperature and pressure. The rate of radioactive disintegration (Activity) is represented as -(dN)/(dt)=lambdaN Where lambda= decay constant, N= number of nuclei at time t, N_(0) =initial no. of nuclei. The above equation after integration can be represented as lambda=(2.303)/(t)log((N_(0))/(N)) Half-life period of U is 2.5xx10^(5) years. In how much time will the amount of U^(237) remaining be only 25% of the original amount ? a) 2.5xx10^(5) year b) 1.25xx10^(5) years c) 5xx10^(5) years d) none of these by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CHEMICAL KINETIC & NUCLEAR CHEMISTRYBOOK - NARENDRA AWASTHICHAPTER - CHEMICAL KINETIC & NUCLEAR CHEMISTRYEXERCISE - Level 1 (Q.3 To Q.32)
1 Videos
- CHEMICAL KINETIC & NUCLEAR CHEMISTRYBOOK - NARENDRA AWASTHICHAPTER - CHEMICAL KINETIC & NUCLEAR CHEMISTRYEXERCISE - Level 1 (Q.33 To Q.62)
2 Videos
- SURFACE CHEMISTRYBOOK - NARENDRA AWASTHICHAPTER - SURFACE CHEMISTRYEXERCISE - Level -2
1 Videos
Similar Questions
The following data pertain to reaction between A and B
S.No[A][B]RatemolL−1molL−1molL−1sec−1I1×10−22×10−22×10−4II2×10−22×10−24×10−4III2×10−24×10−28×10−4
Which of the following interference(s) can be drawn from the above data
(a) Rate constatnt of the reaction 10−4
(b) Rate law of reaction is k[A][B]
(c ) Rate of reaction increases four times on doubling the concentration of both the reactant Select the correct answer codes:
a) a,b and C
b) a and b
c) b and c
d) c alone
View Solutioncolumn Icolumn IIP.Zero order reaction1.t1/2α1[A]0Q.First order reaction2.t100%=[A]0/kR.second order reactions3.Involves at least two reactantsS.Pseudo unimolecular reaction4.[A]=[A]0e−kt
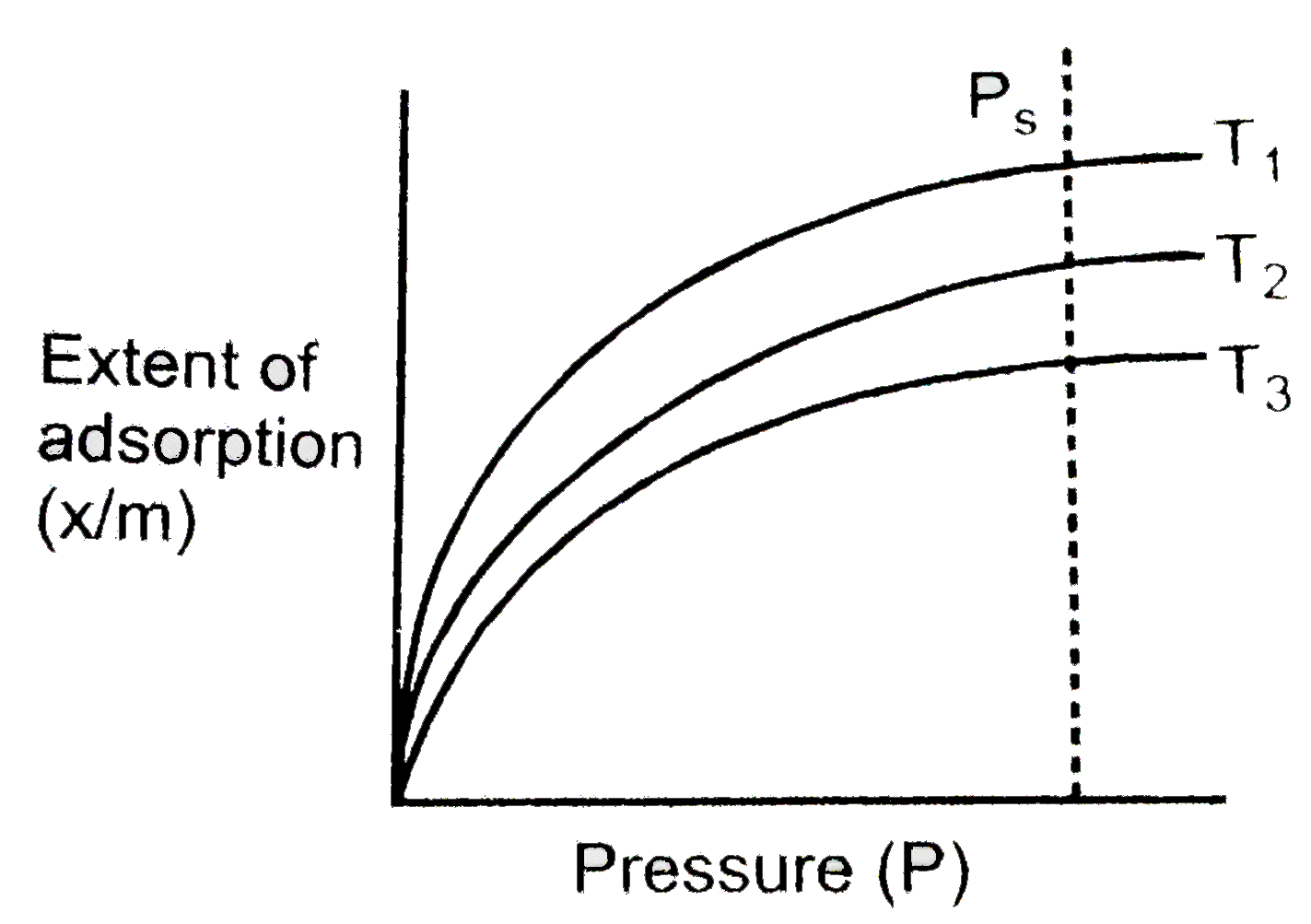
View Solutionfor the graph below, select correct order of temperture ?
View SolutionNuclei of a radioactive element X are being produced at a constant rate K and this element decays to a stable nucleus Y with a decay constant lambda and half-life T_(1//3) . At the time t=0 , there are N_(0) nuclei of the element X . The number N_(X) of nuclei of X at time t=T_(1//2) is .
View SolutionRadioactive disintegration is a first order reaction and its rate depends only upon the nature of nucleus and does not depend upon external factors like temperature and pressure. The rate of radioactive disintegration (Activity) is represented as
−dNdt=λN Where λ= decay constant, N= number of nuclei at time t, N0 =intial no. of nuclei. The above equation after integration can be represented as
λ=2.303tlog(N0N)
Half-life period of U2.5×105 years. In how much thime will the amount of U237 remaining be only 25% of the original amount ?
View SolutionRadioactive disintegration is a first order reaction and its rate depends only upon the nature of nucleus and does not depend upon external factors like temperature and pressure. The rate of radioactive disintegration (Activity) is represented as
−dNdt=λN Where λ= decay constant, N= number of nuclei at time t, N0 =intial no. of nuclei. The above equation after integration can be represented as
λ=2.303tlog(N0N)
Calculate the half-life period of a radioactive element which remains only 1/16 of its original amount in 4740 years:
View SolutionRadioactive disintegration is a first order reaction and its rate depends only upon the nature of nucleus and does not depend upon external factors like temperature and pressure. The rate of radioactive disintegration (Activity) is represented as -(dN)/(dt)=lambdaN Where lambda= decay constant, N= number of nuclei at time t, N_(0) =intial no. of nuclei. The above equation after integration can be represented as lambda=(2.303)/(t)log((N_(0))/(N)) What is the activity in Ci (curie) of 1.0mole plutonium -239 ? (t_(1//2)=24000 yeasrs)
View SolutionRadioactive disintegration is a first order reaction and it's rate depends only upon the nature of nucleus and does not depend upon external factors like temoperature an pressure. The rate of radioactive disintigration (Activity) is respresented as −d(N)dt=λN
Where λ=decay consatant, N= number of nuclei at time t, N0=initial no. of nucleei. The above equation after integration can be represented as
λ=2.303tlog.N0N
Half-life period of U237 is 2.5×105 years. In how much time will the amount of U237 remaining be only 25% of the original amount?
View SolutionRadioactive disintegration is a first order reaction and it's rate depends only upon the nature of nucleus and does not depend upon external factors like temoperature an pressure. The rate of radioactive disintigration (Activity) is respresented as −d(N)dt=λN
Where λ=decay consatant, N= number of nuclei at time t, N0=initial no. of nucleei. The above equation after integration can be represented as
λ=2.303tlog.N0N
Calculate the half-life period of a radioactive element which remains only 1/16 of it's original amount in 4740 years:
View SolutionRadioactive disintegration is a first order reaction and it's rate depends only upon the nature of nucleus and does not depend upon external factors like temoperature an pressure. The rate of radioactive disintigration (Activity) is respresented as (-d(N))/(dt)=lambdaN Where lambda =decay consatant, N= number of nuclei at time t, N""_(0) =initial no. of nucleei. The above equation after integration can be represented as lamda=2.303/tlog.(N""_(0))/(N) What is the activity in Ci(curie) of 1.0 mole of plutonium-239?
View SolutionNuclei of a radioactive element 'A' are being produced at a constant rate alpha the element has a decay constant lambda At time t=0 there are N_(0) nuclei of the element If alpha=2N_(0)lambda the number of nuclei of A after undergone radioactivity decay till time t=(l n2) / lambda :
View SolutionA radioactive nuclide is produced at a constant rate of α− per second. It decay constant is λ . If N0 be the no. of nuclei at time t = 0 , then maximum no. of nuclei possible are
View SolutionRadioactive disintegration is a first order reaction and it's rate depends only upon the nature of nucleus and does not depend upon external factors like temperature and pressure . The rate of radioactive disintegration (Activity) is represented as - (dN)/(dt) = lambda N , Where lambda = decay constant , N number of nuclei at time t , N_(0) = initial no. of nuclei. The above equation after integration can be represented as lambda = (2.303)/(t) "log" ((N_(0))/(N)) Half-life period of U^(232) is 2.5 xx 10^(5) years . In how much time will the amount of U^(237) remaining be only 25% of the original amount ?
View SolutionRadioactive disintegration is a first order reaction and it's rate depends only upon the nature of nucleus and does not depend upon external factors like temperature and pressure . The rate of radioactive disintegration (Activity) is represented as - (dN)/(dt) = lambda N , Where lambda = decay constant , N number of nuclei at time t , N_(0) = initial no. of nuclei. The above equation after integration can be represented as lambda = (2.303)/(t) "log" ((N_(0))/(N)) Calculate the half-life period of a radioactive element which remains only 1/16 of it's original amount in 4740 years :
View SolutionRadioactive disintegration is a first order reaction and it's rate depends only upon the nature of nucleus and does not depend upon external factors like temperature and pressure . The rate of radioactive disintegration (Activity) is represented as −dNdt=λN , Where λ = decay constant , N number of nuclei at time t , N0 = initial no. of nuclei.
The above equation after integration can be represented as λ=2.303tlog(N0N)
What is the activity in Ci (curie) of 1.0 mole of Plutonium - 239 ? (t1/2=24,000 years)
View Solution
