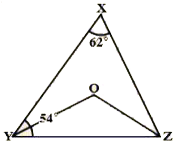
In the given fig.
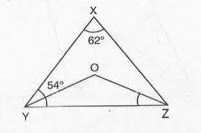 ∠X=62∘, ∠XYZ=54∘. If YO and ZO are the bisectors of ∠XYZ and ∠XZY respectively of ΔXYZ, find ∠OZY and ∠YOZ.Solution in Punjabi
∠X=62∘, ∠XYZ=54∘. If YO and ZO are the bisectors of ∠XYZ and ∠XZY respectively of ΔXYZ, find ∠OZY and ∠YOZ.Solution in Punjabi
32∘,121∘
45∘,115∘
38∘,122∘
46∘,124∘.
Step by step video & image solution for In the given fig. angleX = 62^@, angleXYZ = 54^@. If YO and ZO are the bisectors of angleXYZ and angleXZY respectively of DeltaXYZ, find angleOZY and angleYOZ. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The cost of a note book is twice the cost of a pen. Write a linear equation in two variables to represent this statement.
View SolutionIs zero a rational number ? Can you write in the form pq where p and q are integers and q≠0 ?
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View Solutionआकृति में , ∠X=62∘ और ∠XYZ=54∘ है । यदि YO और ZO क्रमश : ΔXYZ के ∠XYZ और∠XZY के समद्विभाजक है , तो ∠OZY और ∠YOZज्ञात कीजिए ।
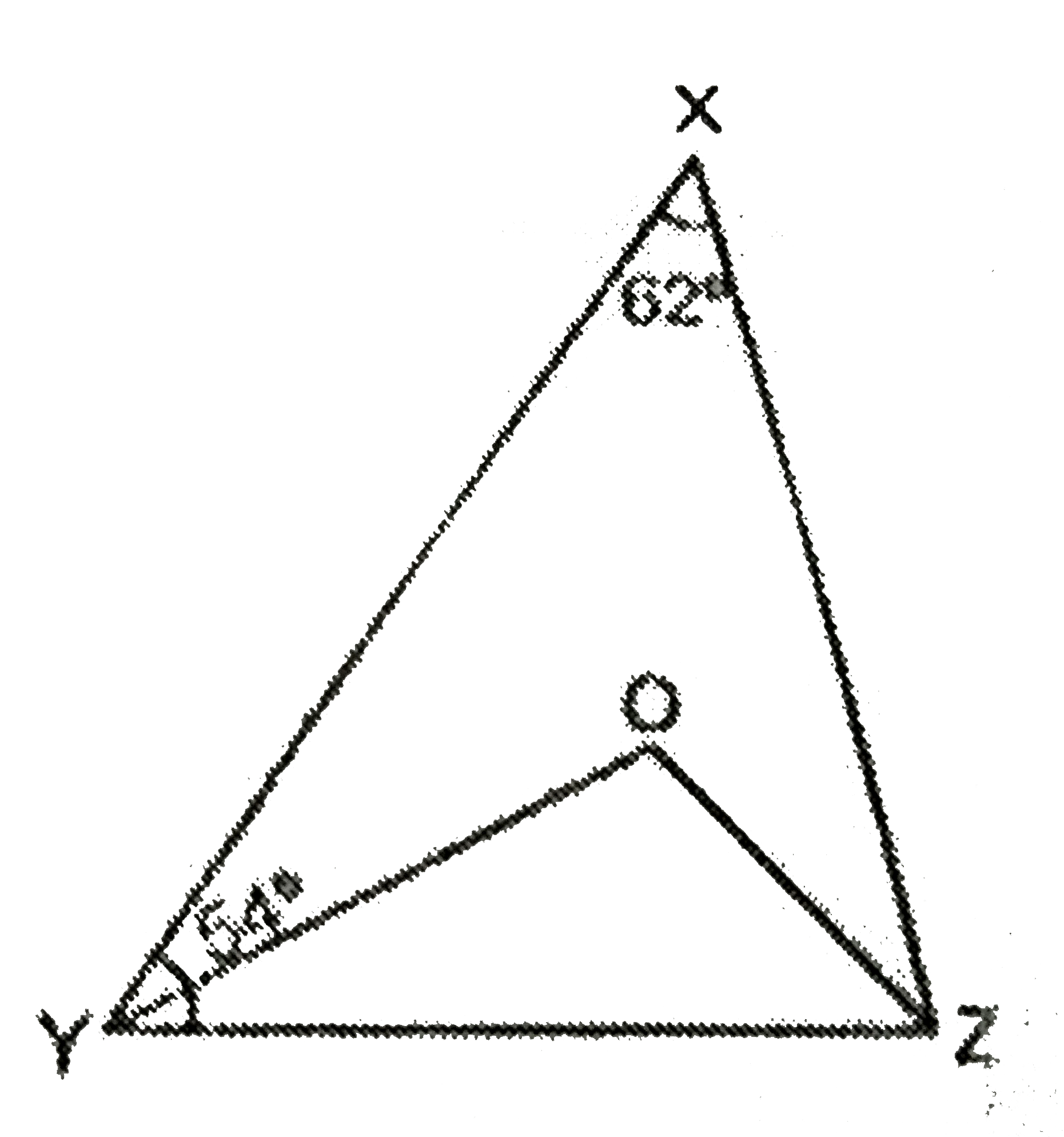
View Solutionआकृति में ∠X=62∘ और ∠XYZ=54∘ है। यदि YO और ZO क्रमशः ΔXYZ के ∠XYZ और ∠XZY के समद्विभाजक हैं, तो ∠OZY का मान क्या होगा ?
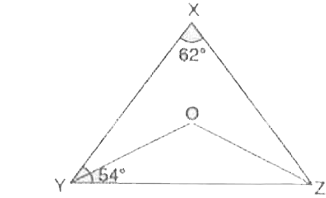
View SolutionIn the picture angleX = 62^@ , angleXYZ = 54^@ triangleXYZ At YO and ZO respectively angleXYZ And angleXZY If the angles are, OZY And angleYOZ Find out.
View SolutionFrom the figure find x and y.
View SolutionIn the given figure, ∠X=62∘,∠XYZ=54∘. In ΔXYZ If YO and ZO are the bisectors of ∠XYZ and ∠XZY respectively find ∠OZY and ∠YOZ
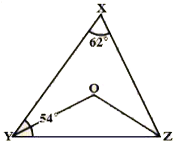
View SolutionIn the given figure, ∠X=62∘,∠XYZ=54∘. In ΔXYZ If YO and ZO are the bisectors of ∠XYZ and ∠XZY respectively find ∠OZY and ∠YOZ
View SolutionIn the given figure, ∠X=62∘,∠XYZ=54∘. In ΔXYZ If YO and ZO are the bisectors of ∠XYZ and ∠XZY respectively find ∠OZY and ∠YOZ
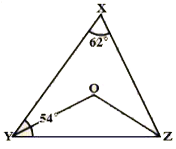
View Solution
