ABCD is a parallelogram whose diagonals intersect at E. AC is produced to F such that CF = AE Prove that ar (ΔBDF) = ar (∣∣gmABCD).Solution in Punjabi
Step by step video & image solution for ABCD is a parallelogram whose diagonals intersect at E. AC is produced to F such that CF = AE Prove that ar (DeltaBDF) = ar (|| gm ABCD). by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
I travelled 432 km by car and 48 litres of the petrol was consumed. I have to go at a place which is 180 km far. How much litres of the petrol is needed for it ?
View SolutionThe centre of a circle lies in .............. of the circle.
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way thatar(AOD)=ar(BOC).Prove that ABCD is a trapezium.
View SolutionIf ABCD is a parallelogram, the prove that ar(ABD)=ar(BCD)=ar(ABC)=ar(ACD)=1/2a r(∣∣gmA B C D)
View SolutionE and F are points on diagonal AC of a parallelogram ABCD such that AE=CF. Show that BFDE is a parallelogram.
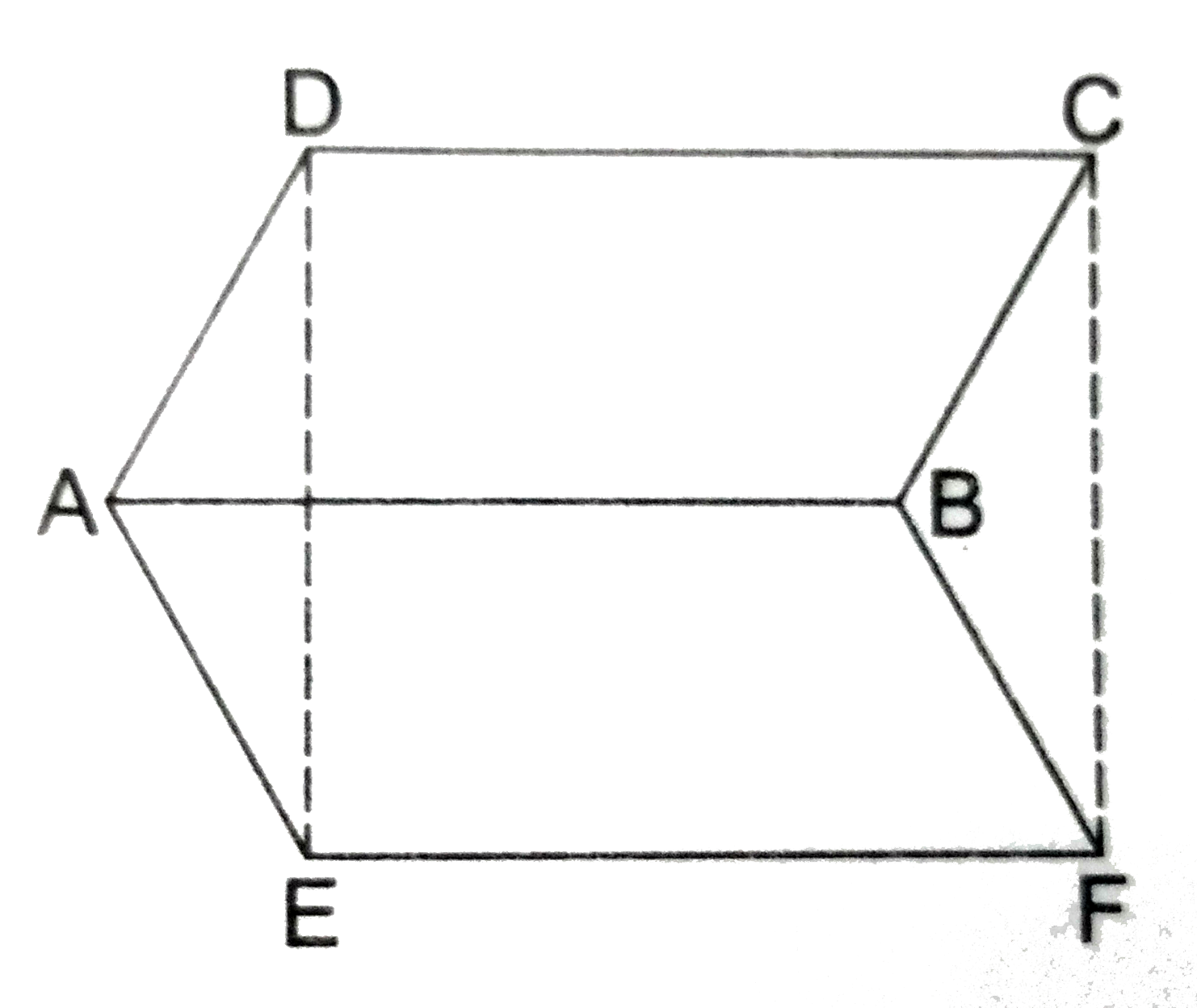
View SolutionIn the adjoing figure, two parallelograms ABCD and AEFB are drawn on opposite sides of AB. Prove that
ar(||gm ABCD)+ar(||gm AEFB)
=ar(||gm EFCD).
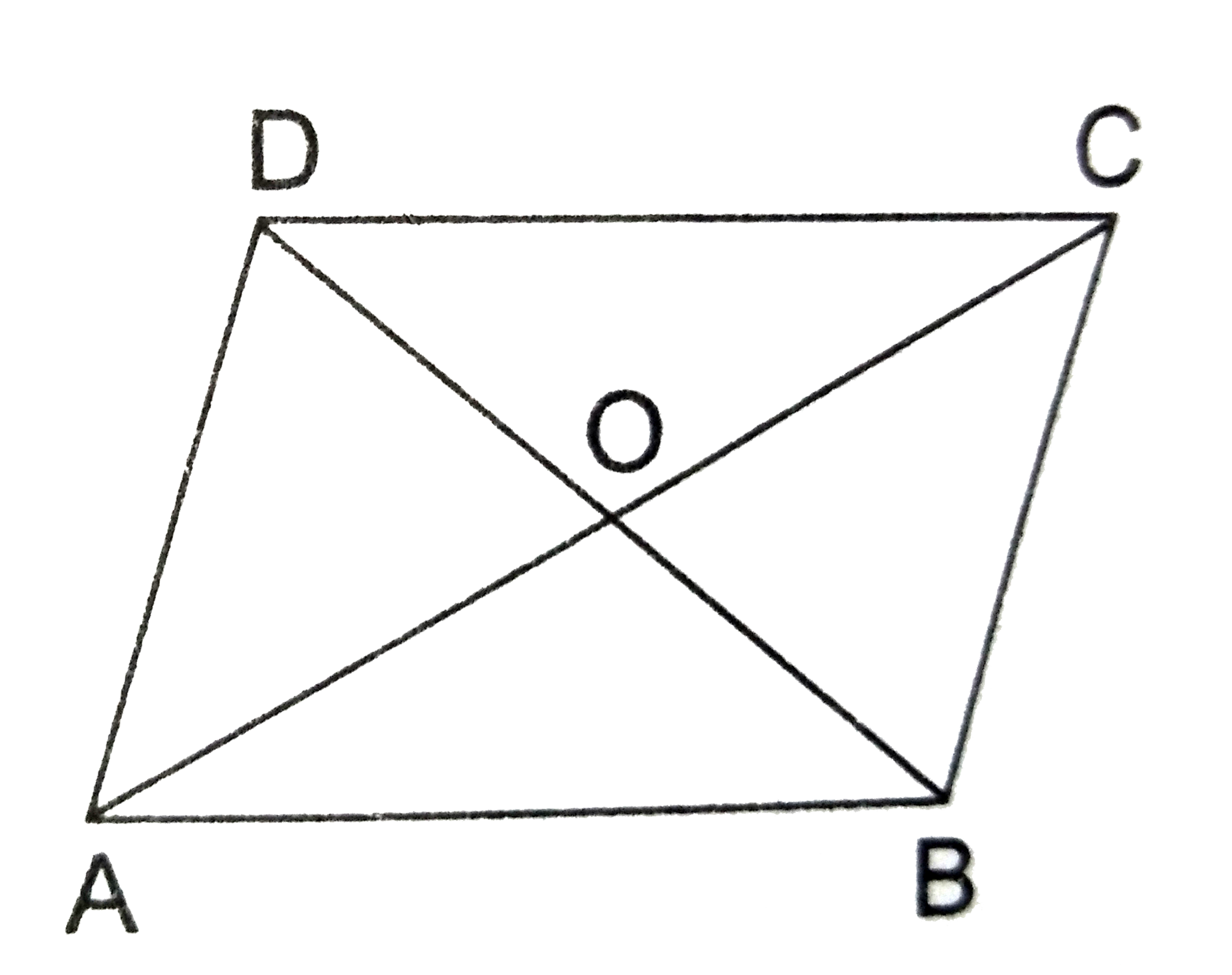
View SolutionIn the given figure, ABCD is a ||gm in which diagonals AC and BD intersect at O. If ar(||gm ABCD) is 52cm2 then the ar(△AOB)=?
View Solutionएक चतुर्भुज ABCD के विकर्ण AC तथा BD परस्पर O पर इस प्रकार प्रतिच्छेद करते हैं कि ar(ΔAOD)=ar(ΔBOC) है । सिद्ध करों कि ABCD एक समलम्ब है।
View Solutionयदि ABCD एक समांतर चतुर्भुज है, तो सिद्ध कीजिए कि
ar(ΔABD)=ar(ΔBCD)=ar(ΔABC)=ar(ΔACD)=12ar(||gmABCD)
View SolutionABCD एक समांतर चतुर्भुज है जिसके विकर्ण O पर प्रतिच्छेद करते है। यदि BO पर कोई बिंदु P हो तो सिद्ध कीजिए कि :
(i)ar(ΔADO)=ar(ΔCDO) (ii)ar(ΔABP)=ar(ΔCBP)
View Solutionएक चतुर्भुज ABCD के विकर्ण AC और BD परस्पर बिन्दु O पर इस प्रकार प्रतिच्छेद करते है कि ar(AOD) = ar(BOC) है। सिद्ध कीजिए कि ABCD एक समलम्ब है।
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar (AOD) = ar (BOC) . Prove that ABCD is a trapezium.
View SolutionABCD एक समांतर चतुर्भुज है जिसके विकर्ण E बिंदु प्रतिच्छेद करते है। AC को F तक इस तरह बढाया गया हैं कि CF = AE सिध्द कीजिए। कि ar (ΔBDF)=ar(∣∣gmABCD)
View SolutionE and F are points on diagonal AC of a parallelogram ABCD such that AE=CF. Show that BFDE is a parallelogram.
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar (AOD) = ar (BOC). Prove that ABCD is a trapezium.
View SolutionABCD is a parallelogram whose diagonals intersect at E. AC is produced to F such that CF = AE Prove that ar (ΔBDF) = ar (∣∣gmABCD).
View Solution
