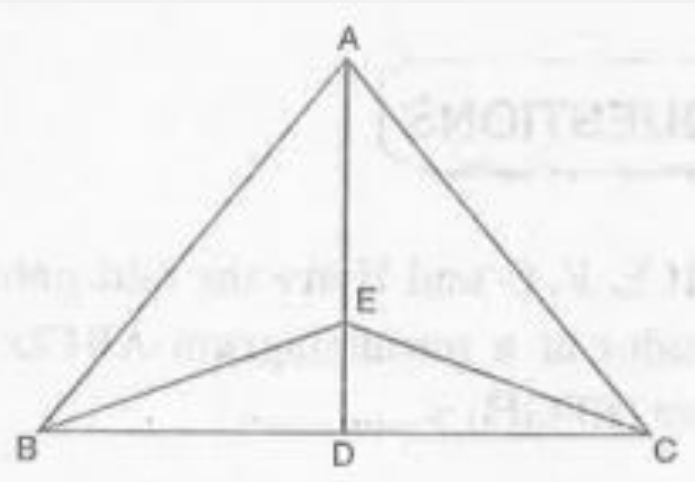
E is any point on median AD of ΔABC. If ar (ΔABE)=10cm2 then ar (ΔACE) is :
 Solution in Punjabi
Solution in Punjabi
20cm2
5cm2
30cm2
10cm2.
Step by step video & image solution for E is any point on median AD of DeltaABC. If ar (DeltaABE) = 10 cm^2 then ar (DeltaACE) is : by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
I travelled 432 km by car and 48 litres of the petrol was consumed. I have to go at a place which is 180 km far. How much litres of the petrol is needed for it ?
View SolutionThe centre of a circle lies in .............. of the circle.
View SolutionWhich of the following are correct chain isomers of butane ? (i)
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionDtermine the images of the following figure about the given line :
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionAt point P, the value of (dy)/(dx) is : ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_R04_E01_025_Q01.png" width="80%"gt
View SolutionIn a triangle ABC (see figure), E is the midpoint of median AD, show that
(i) ar ΔABE=arΔACE
(ii) arΔABE=14ar(ΔABC)
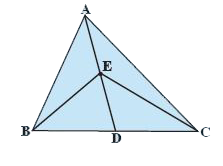
View SolutionIn a triangle ABC (see figure), E is the midpoint of median AD, show that (i) ar DeltaABE = ar DeltaACE (ii) ar DeltaABE=1/4ar(DeltaABC)
View SolutionIn a triangle ABC (see figure), E is the midpoint of median AD, show that
(i) ar ΔABE=arΔACE
(ii) arΔABE=14ar(ΔABC)
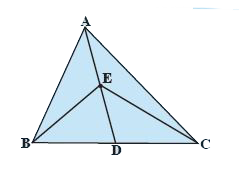
View Solution
