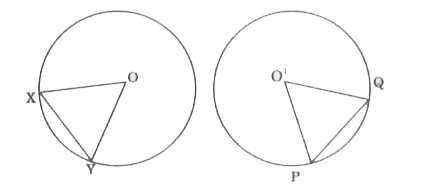
If the angles subtended by the chords of a circle at the centre of the circle are equal, then the chords are equal.Solution in Punjabi
Step by step video & image solution for If the angles subtended by the chords of a circle at the centre of the circle are equal, then the chords are equal. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Match the following:


View SolutionHow will you describe the position of a table lamp on your study table to another person ?
View SolutionProve that if chords of congruent circles subtend equal angles at their centres, then the chords are equal.
View SolutionEqual chords of a circle subtend equal angles at the centre.
View SolutionEqual chords of congruent circles subtend equal angles at the centre.
View SolutionIf the angles subtended by two chords of a circle at the centre are equal, the chords are equal.
View SolutionEqual chord of circle subtends equal angle on centre.
View SolutionIf the angle subtended by two chords of a circle at the centre are equal; the chords are equal.
View SolutionEqual chords of congruent circles subtend equal angles at the centre.
View SolutionThe chord of a circle is equal to its radius, find the angle subtended by this chord at the centre.
View SolutionState and prove that:
Theorem 10.2 : If the angles subtended by the chords of a circle at the centre are equal, then the chords are equal.
View SolutionThe angle subtended at the centre of a circle , by a chord whose length is equal to the radius of the circle will be
View SolutionProve that if chords of congruent circles subtend equal angles at their centre then the chords are equal.
View SolutionProve that equal chords of a circle subtend equal angles at the centre.
View SolutionProve that if chords of congruent circles subtend equal angles at their centres then chords are equal.
View SolutionProve Equal chords of congruent circles subtend equal angles at the centre.
View Solution
