An exhausted chamber with nonconducting walls is connected through a valve to the atmosphere where the pressure is and the temperature is .The valve is openeds lightly and air flows into the chamber until the pressure with in the chamber is .Assuming the air to be have like an ideal gas with constant heat capacities, the final temperature of the air in the chamber is
To find the final temperature of the air in the chamber after it has been filled with air from the atmosphere, we can follow these steps:
Step 1: Understand the System
The chamber is initially evacuated (no air inside), and it is connected to the atmosphere where the pressure is p0 and the temperature is T0. When the valve is opened, air flows into the chamber until the pressure inside the chamber equals p0.
Hint: Recognize that the initial state of the chamber is a vacuum, which means there is no internal energy initially.
Step 2: Apply the First Law of Thermodynamics
The first law of thermodynamics states that the change in internal energy of a system is equal to the heat added to the system minus the work done by the system. In this case, since the chamber is non-conducting, we can assume no heat transfer occurs (adiabatic process).
The initial internal energy U1 is zero (since the chamber is evacuated), and the final internal energy U2 can be expressed in terms of the mass of air m2 and the specific internal energy u2.
Step 3: Relate Internal Energy and Enthalpy
Since the air is flowing in at constant pressure, we can use the concept of enthalpy. The enthalpy change can be related to the internal energy change and the work done by the system.
The equation can be expressed as:
m2u2=m2hb
where hb is the specific enthalpy of the air at pressure p0.
Step 4: Use the Ideal Gas Law
For an ideal gas, the relationship between specific heat capacities is given by:
Cp=Cv+R
where R is the gas constant. The ratio of specific heats is defined as:
γ=CpCv
Step 5: Solve for Final Temperature
From the energy conservation equation, we can express the final temperature Tf in terms of the initial temperature T0:
m2u2=m2⋅CvCp⋅T0
This simplifies to:
Tf=CpCv⋅T0=γT0
Conclusion
Thus, the final temperature of the air in the chamber after it has reached equilibrium with the atmosphere is:
Tf=γT0
---
The chamber is initially evacuated (no air inside), and it is connected to the atmosphere where the pressure is p0 and the temperature is T0. When the valve is opened, air flows into the chamber until the pressure inside the chamber equals p0.
The first law of thermodynamics states that the change in internal energy of a system is equal to the heat added to the system minus the work done by the system. In this case, since the chamber is non-conducting, we can assume no heat transfer occurs (adiabatic process).
Since the air is flowing in at constant pressure, we can use the concept of enthalpy. The enthalpy change can be related to the internal energy change and the work done by the system.
m2u2=m2hb
where hb is the specific enthalpy of the air at pressure p0.
For an ideal gas, the relationship between specific heat capacities is given by:
Cp=Cv+R
where R is the gas constant. The ratio of specific heats is defined as:
γ=CpCv
From the energy conservation equation, we can express the final temperature Tf in terms of the initial temperature T0:
m2u2=m2⋅CvCp⋅T0
This simplifies to:
Tf=CpCv⋅T0=γT0
Thus, the final temperature of the air in the chamber after it has reached equilibrium with the atmosphere is:
Tf=γT0
Similar Questions
A spherical container made of non conducting wall has a small orifice in it. Initially air is filled in it at atmospheric pressure (P0) and atmospheric temperature (T0). Using a small heater, heat is slowly supplied to the air inside the container at a constant rate of H J/s. Assuming air to be an ideal diatomic gas find its temperature as a function of time inside the container.
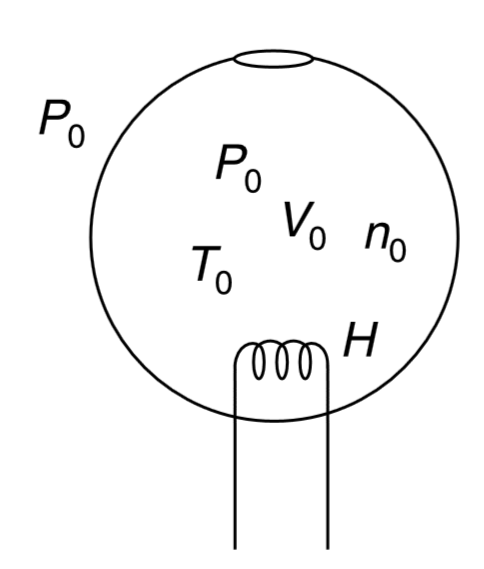 View Solution
View SolutionDry air at 150C and 10 atm is suddenly released at atmospheric pressure. Find the final temperature of the air [CpCv=1.41].
View Solution
Knowledge Check
- Question 1 - Select One
If increase in temperature and volume of air ideal gas is two times, then intitial pressure of P changes to:
A4PB2PCPD3P - Question 2 - Select One
An insulated container of gas has two chambers separated by an insulating partition. One of the chmabers has volume V1 and contains ideal gas at pressure P1 and temperature T1.The other chamber has volume V2 and contains ideal gas at pressure P2 and temperature T2. If the partition is removed without doing any work on the gas, the final equilibrium temperature of the gas in the container will be
A(T1T2P1V1+P2V2P1V1T2+P2V2T1BP1V1T1+P2V2T2P1V1+P2V2CP1V1T2+P2V2T1P1V1+P2V2DT1T2(P1V1+P2V2)P1V1T1+P2V2T2 - Question 3 - Select One
An insulated container of gas has two chambers separated by an insulating partition. One of the chambers has volume V1 and contains ideal gas at pressure P1 and temperature T1. The other chambers has volume V2 and contains ideal gas at pressure P2 and temperature T2. If the partion is removed without doing any work on the gas, the final equilibrium temperature of the gas in the container will be
AT1T2(P1V1+P2V2)P1V1T2+P2V2T1BP1V1T1+P2V2T2P1V1+P2V2CP1V1T2+P2V2T1P1V1+P2V2DT1T2(P1V1+P2V2)P1V1T1+P2V2T2
A cylindrical container is divided into three parts by two tight fitting pistons. The pistons are connected by a spring. The region between the pistons is vacuum and the other two parts have same number of moles of an ideal gas. Initially, both the gas chambers are at temperature T0 and the spring is compressed by 1 m. Length of both gas chambers is 1 m in this position. Now the temperature of the left and right chambers are raised to 4T03 and 5T03 respectively. Find the final compression in the spring in equilibrium. Assume that the pistons slide without friction
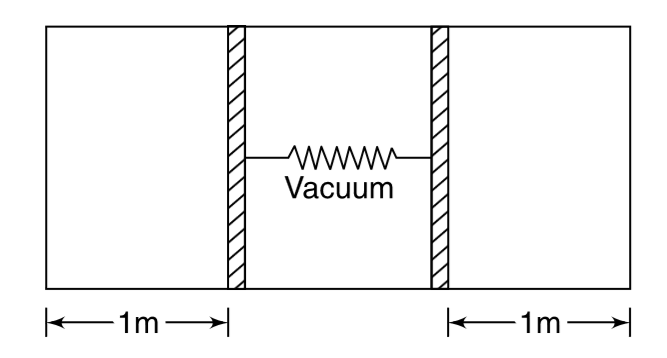 View Solution
View SolutionA sample of gas in a box is at pressure P0 and temperature T0. If number of molecules is doubled and total kinetic energy of the gas is kept constant, then final temperature and pressure will be
View SolutionThe pressure of the gas in a cylindrical chamber is p0. The vertical force exerted by the gas on its hemispherical end is
 View Solution
View SolutionAn open vessel at 27∘C is heated untill two fifth of the air (assumed as an ideal gas) in it has escaped from the vessel. Assuming that the volume of the vessel remains constant, the temperature at which the vessel has been heated is :
View Solution4 moles of an ideal gas is at 0∘C . At constant pressure it is heated to double its volume, then its final temperature will be
View Solution

