दिलेल्या आकृतीमध्ये $∠ P Q R$ = $90^{\circ}$ , $∠ P Q S$ = $90^{\circ}$ $∠ P R Q$ = $α$ व $∠ Q P S$ = $θ$ , तर खालील त्रिकोणमितीय गुणोत्तरे लिहा.
$sin α$ , $cos α$ , $tan α$

Video Solution

Answer

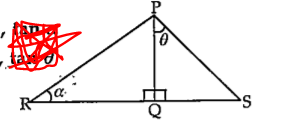
Step by step video & image solution for दिलेल्या आकृतीमध्ये angle PQR =90^@, angle PQS = 90^@ angle PRQ= alpha व angle QPS = theta, तर खालील त्रिकोणमितीय गुणोत्तरे लिहा. sin alpha, cos alpha, tan alpha by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.

Updated on:21/07/2023

Class 9 MATHS त्रिकोणमिती

दिलेल्या आकृतीमध्ये ∠PQR =90∘, ∠PQS = 90∘ ∠PRQ= α व ∠QPS = θ, तर खालील त्रिकोणमितीय गुणोत्तरे लिहा. sinα, cosα, tanα

Topper's Solved these Questions

Similar Questions

NIKITA PUBLICATION MARATHI-त्रिकोणमिती -EXAMPLES

दिलेल्या आकृतीमध्ये $∠ P Q R$ = $90^{\circ}$ , $∠ P Q S$ = $90^{\circ}$ $∠ P R Q$ = $α$ व $∠ Q P S$ = $θ$ , तर खालील त्रिकोणमितीय गुणोत्तरे लिहा.
$sin α$ , $cos α$ , $tan α$