Question

ग्राफ़िय विधि से साबित करे कि ${\displaystyle s=ut+\frac{1}{2}a{t}^2,}$ जहाँ s,u,a और t अपना सामान्य अर्थ रखते है ।

Explanation

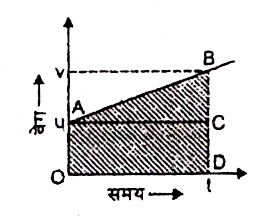
मान लिया कि किसी समयांतराल के प्रारंभ में किसी वस्तु का वेग ॥ तथा समयांतराल 1 के अंत में v है, यदि वस्तु एक समान वेग से जा रही है तो इसका वेग-समय ग्राफ सरल रेखा होगा (जैसा कि चित्र में दिखाया गया है।) एकसमान त्वरण के साथ रेखा पर गतिमान वस्तु द्वारा समय में तय की हुयी दूरी।
वेग-समय ग्राफ से, O से t समयांतराल में समयतय की हुयी दूरी छायांकित (shaded) भाग के क्षेत्रफल के बराबर होगी।
दूरी s = समलंब चतुर्भुज OBAD का क्षेत्रफल = आयत OBCD का क्षेत्रफल + त्रिभुज ABC का क्षेत्रफल
`= OBxx OD+1/2+BCxxAC`
`=u.t+1/2 (a.t)t[ :. (AB)/(BC) =a " तथा " BC=t]`
`impliess =ut +1/2 at^2`