What must be the angle with respect to the incident light at which he should place the mirrors?
To determine the angle at which the mirrors should be placed with respect to the incident light, we can follow these steps:
1. Understanding the Problem: We need to find the angle at which mirrors should be oriented to reflect light from an object (point A) to an observer (point I) through a series of reflections.
2. Identifying the Path of Light: The light ray travels from point A to point I. We denote the points where the mirrors will be placed as P, Q, and R. The ray will reflect off these mirrors to reach the observer.
3. Placing the First Mirror (M1):
- The first mirror (M1) is placed at point P.
- The incoming ray from point A strikes mirror M1 at an angle of incidence (let's denote it as θ).
- According to the law of reflection, the angle of reflection is equal to the angle of incidence.
4. Placing the Second Mirror (M2):
- The second mirror (M2) is placed at point Q.
- The ray reflected from M1 now strikes M2.
- Again, the angle of incidence at M2 will equal the angle of reflection.
5. Placing the Third Mirror (M3):
- The third mirror (M3) is placed at point R.
- The ray reflected from M2 strikes M3, and the same law of reflection applies.
6. Calculating the Angles:
- The total angle between the incoming ray and the outgoing ray after reflecting off all mirrors must equal 90 degrees.
- Since there are two reflections (from M1 to M2 and from M2 to M3), the total angle of deviation is 90 degrees.
- Therefore, the angle between the incident ray and the normal to the mirror at each reflection point must be 45 degrees.
7. Conclusion:
- Each mirror should be placed at an angle of 45 degrees with respect to the incident light. This ensures that the light ray can be redirected properly to reach the observer.
Final Answer:
The mirrors should be placed at an angle of 45 degrees with respect to the incident light.
---
- The first mirror (M1) is placed at point P.
- The incoming ray from point A strikes mirror M1 at an angle of incidence (let's denote it as θ).
- According to the law of reflection, the angle of reflection is equal to the angle of incidence.
- The second mirror (M2) is placed at point Q.
- The ray reflected from M1 now strikes M2.
- Again, the angle of incidence at M2 will equal the angle of reflection.
- The third mirror (M3) is placed at point R.
- The ray reflected from M2 strikes M3, and the same law of reflection applies.
- The total angle between the incoming ray and the outgoing ray after reflecting off all mirrors must equal 90 degrees.
- Since there are two reflections (from M1 to M2 and from M2 to M3), the total angle of deviation is 90 degrees.
- Therefore, the angle between the incident ray and the normal to the mirror at each reflection point must be 45 degrees.
- Each mirror should be placed at an angle of 45 degrees with respect to the incident light. This ensures that the light ray can be redirected properly to reach the observer.
The mirrors should be placed at an angle of 45 degrees with respect to the incident light.
Topper's Solved these Questions
Similar Questions
Figures shows a plane mirror on which a light ray is incident, if the incident light ray is turned by 10∘ and the mirror by 20∘ as shown , find the angle turned by the reflected ray.
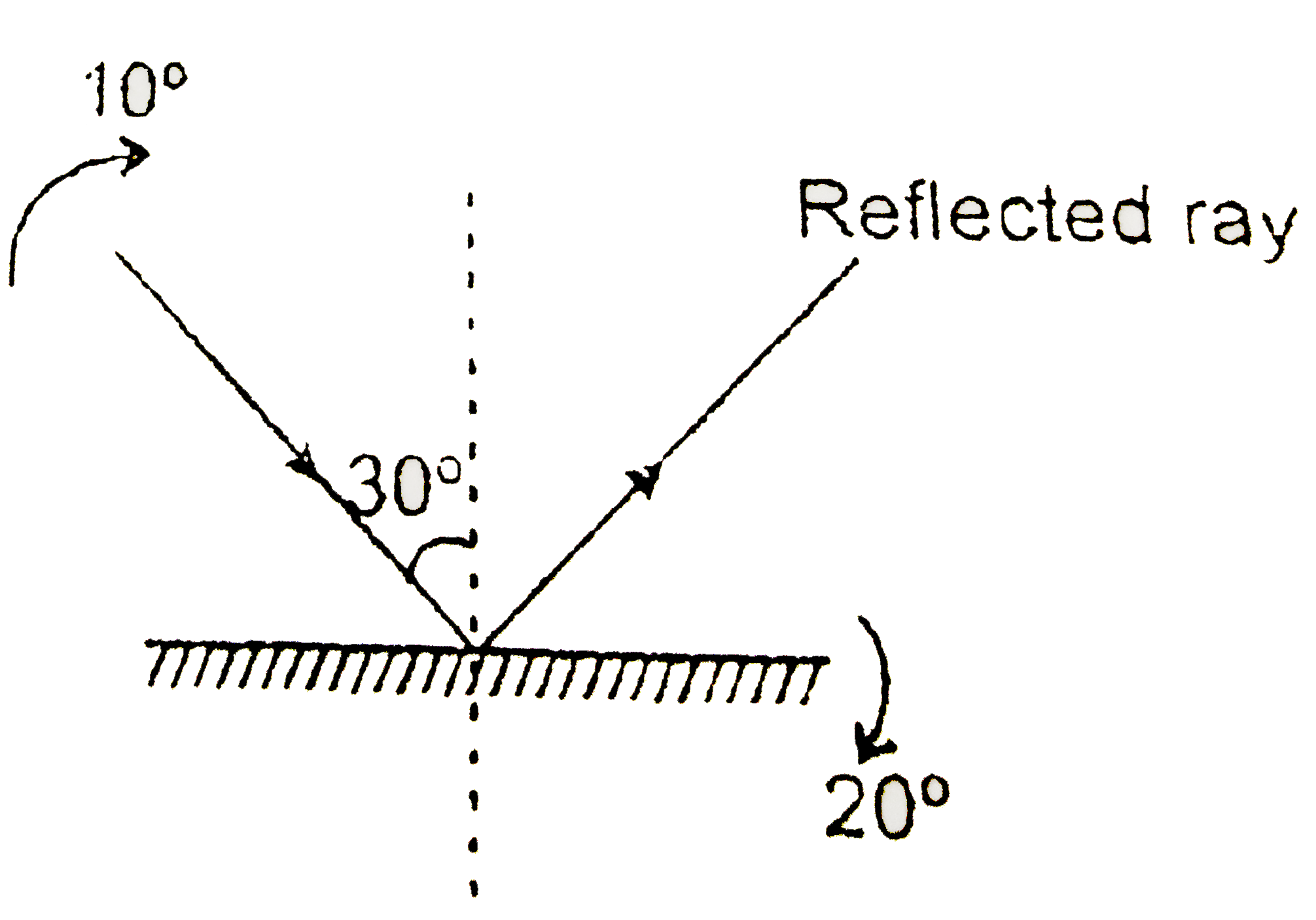
View SolutionA student holding a mirror in his hand, directed the reflecting surface of the mirror towards the Sun. He then directed the reflected light on to a sheet of paper held close to the mirror.
What should he do to burn the paper ?
View Solution
Knowledge Check
Read the following statements and choose the correct option.
(A) The angle made by the incident light ray with the plane of mirror is equal to the angle made by the reflected light ray with the plane of mirror.
(B) The angle between an incident light ray and a reflected light ray is twice that of the angle between the incident light ray and normal.AOnly A is trueBOnly B is trueCBoth A and B are trueDBoth A and B are falseRead the following statements and choose the correct option.
(A) The angle made by the incident light ray with the plane of mirror is equal to the angle made by the reflected light ray with the plane of mirror.
(B) The angle between an incident light ray and a reflected light ray is twice that of the angle between the incident light ray and normal.AOnly A is trueBOnly B is trueCBoth A and B are trueDBoth A and B are falseThe angle which the incident ray makes with the mirror is called
Aangle of incidenceBangle of reflectionCright angleDglancing angle of incidence
A ray of light is incident on a plane mirror at an angle of 40∘ with respect to surface normal. When it gets reflected from the mirror, it undergoes a deviation of
View SolutionFigure shows a plane mirror onto which a light rays is incident. If the incident light ray is rotated by 10∘ and the mirror by 20∘, as show in figure below, find the angle by which the reflected ray is rotated.
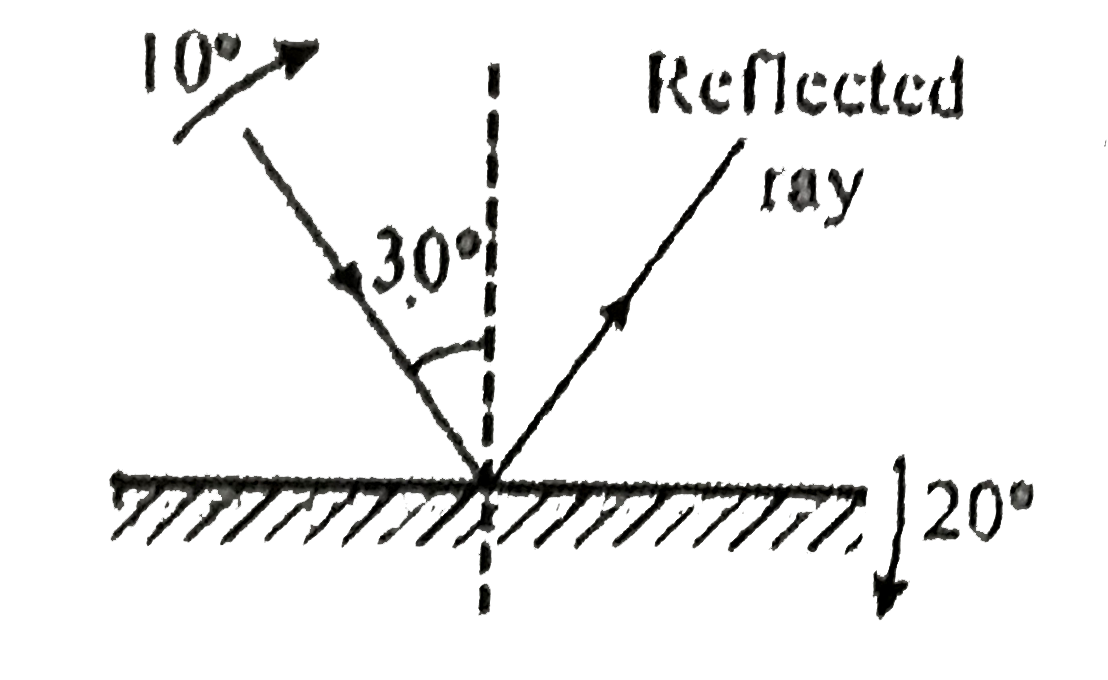
View SolutionA ray of light is incident on a plane mirror, making an angle 'q' with the surface of the mirror. Arrange the following steps in sequential order to calculate the angle between the incident light ray and the reflected light ray.
(A) Draw a normal line on the plane mirror at the point of incidence of the light ray.
(B) Note down the angle between the plane mirror and the incident light ray.
(C) The sum of the angle of incidence and the angle between the plane mirror and the incident ray is 90∘.Determine the angle of incidence.
(D) From the laws of reflection, the angle of incidence is equal to the angle of reflection. Then the sum of the angle of incidence and the angle of reflection gives the angle between the incident light ray and the reflected light ray.
View SolutionA ray of light is incident on a plane mirror, making an angle 'q' with the surface of the mirror. Arrange the following steps in sequential order to calculate the angle between the incident light ray and the reflected light ray.
(A) Draw a normal line on the plane mirror at the point of incidence of the light ray.
(B) Note down the angle between the plane mirror and the incident light ray.
(C) The sum of the angle of incidence and the angle between the plane mirror and the incident ray is 90∘.Determine the angle of incidence.
(D) From the laws of reflection, the angle of incidence is equal to the angle of reflection. Then the sum of the angle of incidence and the angle of reflection gives the angle between the incident light ray and the reflected light ray.
View SolutionA light ray is made to incident on a mirror. If the glancing angle of incidence is 30∘, then write the following steps in sequence to find the angle between the incident light ray and the reflected light ray.
(a) Note the glancing angle of incidence from the given information.
(b) The angle of reflection is equal to the angle of incidence.
(c) The angle of incidence ∠i will be equal to (90∘−30∘).
(d) The angle between the incident light ray and the reflected light ray is equal to 2∠i or 2(90∘−∠30∘).
View Solution
