Question

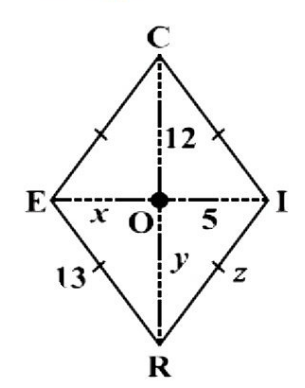
If RICE is a rhombus with EC = 20 cm and OC = 12 cm, can you find x, y, z ?

Explanation

To solve the problem, we need to find the values of x, y, and z in the rhombus RICE, given that EC = 20 cm and OC = 12 cm.

1. Understanding the Rhombus Properties:
In a rhombus, the diagonals bisect each other at right angles. Let's denote the diagonals as EI and RC, where E and R are opposite vertices and I and C are the midpoints of the diagonals.

2. Given Information:
- EC (one diagonal) = 20 cm
- OC (half of diagonal EC) = 12 cm

3. Finding the Length of the Other Diagonal:
Since OC is half of EC, we can denote the full length of diagonal EI as 2y. Therefore, we have:
\( OC = y = 12 \text{ cm} \)
Hence, the full length of diagonal EI is:
\( EI = 2y = 2 \times 12 = 24 \text{ cm} \)

4. Using the Right Triangle Formed by the Diagonals:
In the right triangle formed by the diagonals, we can apply the Pythagorean theorem. The sides of the triangle are:
- Half of EC = x (which we need to find)
- Half of EI = y = 12 cm
- The side of the rhombus (which we denote as z)

According to the properties of the rhombus:
\( z^2 = x^2 + y^2 \)

5. Finding x:
We know that EC = 20 cm, so:
\( x + 2 = 5 \implies x = 5 - 2 = 3 \text{ cm} \)

6. Finding y:
We already established that y = 12 cm.

7. Finding z:
Since all sides of a rhombus are equal, we can say:
\( z = EC = 20 \text{ cm} \)

Summary of Values:
- \( x = 3 \text{ cm} \)
- \( y = 12 \text{ cm} \)
- \( z = 20 \text{ cm} \)