Let D = 3, L = 7 and A = 8. Find the other digits in the sum
M A D+A S+ A¯¯¯¯¯¯¯¯¯¯¯¯¯B U L L–––––––––
Step by step video & image solution for Let D = 3, L = 7 and A = 8. Find the other digits in the sum {:("M A D"),(+"A S"),(+" A"),(ulbar("B U L L")):} by Maths experts to help you in doubts & scoring excellent marks in Class 8 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PLAYING WITH NUMBERS BOOK - NCERT EXEMPLARCHAPTER - PLAYING WITH NUMBERS EXERCISE - Application, Games and Puzzles
1 Videos
- PLAYING WITH NUMBERS BOOK - NCERT EXEMPLARCHAPTER - PLAYING WITH NUMBERS EXERCISE - Think and Discuss
1 Videos
- PLAYING WITH NUMBERS BOOK - NCERT EXEMPLARCHAPTER - PLAYING WITH NUMBERS EXERCISE - Exercise (true (T) or false (F))
11 Videos
- MENSURATIONBOOK - NCERT EXEMPLARCHAPTER - MENSURATIONEXERCISE - THINK AND DISCUSS
2 Videos
- RATIONAL NUMBERS BOOK - NCERT EXEMPLARCHAPTER - RATIONAL NUMBERS EXERCISE - Think and Discuss
1 Videos
Similar Questions
Knowledge Check
Complete the given series : Z d S m b l V q - - - - f S B y.
AN d Y UBm E x VCd n y UDD n Y u
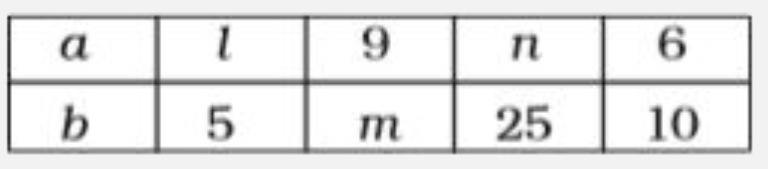
If a and b vary inversely to each other, then find the values of l, m, n.
View SolutionIf L(5,-8) and M (-7,-3) then the distance between points
L and M is _ _ _ _ _ _
View SolutionUsing the s,p,d notations, describe the orbital with the following quantum numbers :
(a)n=1,l=0 (b)n=3,l=2
(c)n=3,l=1 (d)n=2,l=1
(e)n=4,l=3 (f)n=4,l=2.
View SolutionIt is given that l varies directly as m.
Find m when l is 8.
View SolutionLet A={n∈N: n is a 3- digit number }
B={9k+2:k∈N}
and C={9k+l:K∈N} for some l(0<l<9) if the sum of all the elements of the set A∩(B∪C) is 274×400 , then l is equal to ______.
View SolutionA neutral atom of an element has 2k,8L,8L,9M and 2N electrons . Find out the following :
(a) Atomic no.
(b ) total no. of s-electrons ,
(c ) total no. of s-electrons ,
(d) total no. of s-electrons ,
(e ) Valency of element .
(f) No, of unpaired elecrons) .
View SolutionIn a ABC , If LandM are points ABandAC respectively such that LMparallelBC
Prove that: ar(ABM)=ar(ACL)
View Solution
