From given integers in Column I match an integer of Column II so that their product lies between –19 and –6:
Column IColumn II−516−1−738−2
To solve the problem, we need to find pairs of integers from Column I and Column II such that their product lies between -19 and -6. Let's go through the steps systematically.
Step 1: List the integers from both columns
- Column I: -5, 6, -7, 8
- Column II: 1, -1, 3, -2
Step 2: Determine the range for the product
We need the product of the paired integers to be between -19 and -6. This means:
- The product should be greater than -19
- The product should be less than -6
Step 3: Calculate products for each pairing
We will multiply each integer from Column I with each integer from Column II and check if the product lies within the specified range.
1. Pair -5 with each integer in Column II:
- -5 * 1 = -5 (not valid, as it is not less than -6)
- -5 * -1 = 5 (not valid, as it is not negative)
- -5 * 3 = -15 (valid, as it is between -19 and -6)
- -5 * -2 = 10 (not valid, as it is not negative)
2. Pair 6 with each integer in Column II:
- 6 * 1 = 6 (not valid, as it is not negative)
- 6 * -1 = -6 (not valid, as it is not less than -6)
- 6 * 3 = 18 (not valid, as it is not negative)
- 6 * -2 = -12 (valid, as it is between -19 and -6)
3. Pair -7 with each integer in Column II:
- -7 * 1 = -7 (not valid, as it is not less than -6)
- -7 * -1 = 7 (not valid, as it is not negative)
- -7 * 3 = -21 (not valid, as it is not greater than -19)
- -7 * -2 = 14 (not valid, as it is not negative)
4. Pair 8 with each integer in Column II:
- 8 * 1 = 8 (not valid, as it is not negative)
- 8 * -1 = -8 (valid, as it is between -19 and -6)
- 8 * 3 = 24 (not valid, as it is not negative)
- 8 * -2 = -16 (valid, as it is between -19 and -6)
Step 4: List the valid pairs
From our calculations, the valid pairs that yield products between -19 and -6 are:
- (-5, 3) → -15
- (6, -2) → -12
- (8, -1) → -8
- (8, -2) → -16
Final Answer
The pairs that satisfy the condition are:
- (-5, 3)
- (6, -2)
- (8, -1)
- (8, -2)
- Column I: -5, 6, -7, 8
- Column II: 1, -1, 3, -2
We need the product of the paired integers to be between -19 and -6. This means:
- The product should be greater than -19
- The product should be less than -6
We will multiply each integer from Column I with each integer from Column II and check if the product lies within the specified range.
- -5 * 1 = -5 (not valid, as it is not less than -6)
- -5 * -1 = 5 (not valid, as it is not negative)
- -5 * 3 = -15 (valid, as it is between -19 and -6)
- -5 * -2 = 10 (not valid, as it is not negative)
- 6 * 1 = 6 (not valid, as it is not negative)
- 6 * -1 = -6 (not valid, as it is not less than -6)
- 6 * 3 = 18 (not valid, as it is not negative)
- 6 * -2 = -12 (valid, as it is between -19 and -6)
- -7 * 1 = -7 (not valid, as it is not less than -6)
- -7 * -1 = 7 (not valid, as it is not negative)
- -7 * 3 = -21 (not valid, as it is not greater than -19)
- -7 * -2 = 14 (not valid, as it is not negative)
- 8 * 1 = 8 (not valid, as it is not negative)
- 8 * -1 = -8 (valid, as it is between -19 and -6)
- 8 * 3 = 24 (not valid, as it is not negative)
- 8 * -2 = -16 (valid, as it is between -19 and -6)
From our calculations, the valid pairs that yield products between -19 and -6 are:
- (-5, 3) → -15
- (6, -2) → -12
- (8, -1) → -8
- (8, -2) → -16
The pairs that satisfy the condition are:
- (-5, 3)
- (6, -2)
- (8, -1)
- (8, -2)
Topper's Solved these Questions
- INTEGERSBOOK - NCERT EXEMPLARCHAPTER - INTEGERSEXERCISE - (D) APPLICATION (Puzzle)
5 Videos
- INTEGERSBOOK - NCERT EXEMPLARCHAPTER - INTEGERSEXERCISE - THINK AND DISCUSS
13 Videos
- INTEGERSBOOK - NCERT EXEMPLARCHAPTER - INTEGERSEXERCISE - VOCOBULARY
5 Videos
- FRACTIONS AND DECIMALSBOOK - NCERT EXEMPLARCHAPTER - FRACTIONS AND DECIMALSEXERCISE - EXERCISE (FIND THE ERROR)
3 Videos
- LINES AND ANGLES BOOK - NCERT EXEMPLARCHAPTER - LINES AND ANGLES EXERCISE - Exercise (fill in the blanks)
3 Videos
Similar Questions
Match the integer in Column I to an integer in Column II so that the sum is between –11 and –4
View SolutionMatch Column I with Column II

View SolutionMatch Column I with Column II

View SolutionMatch Column I with Column II
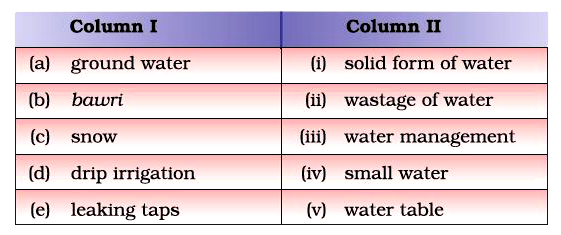
View SolutionMatch Column I with Column II

View SolutionMatch Column I with Column II

View SolutionMatch Column I with Column II .
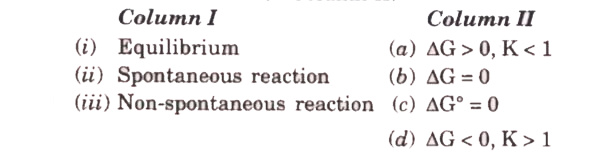
View SolutionMatch Column I with Column II.

View SolutionMatch Column I with Column II:
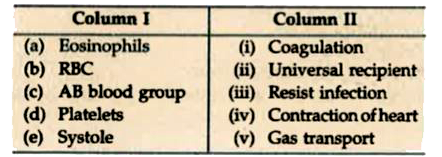
View SolutionMatch Column I with Column II.

View Solution
