Angles which are both supplementary and vertically opposite are
95∘,85∘
90∘,90∘
100∘,80∘
45∘,45∘
The correct Answer is:B
To solve the question, "Angles which are both supplementary and vertically opposite are," we will follow these steps:
Step 1: Understand the Definitions
- Supplementary Angles: Two angles are supplementary if the sum of their measures is equal to 180 degrees.
- Vertically Opposite Angles: When two lines intersect, they form two pairs of opposite angles. These angles are called vertically opposite angles, and they are equal in measure.
Step 2: Set Up the Angles
Let’s denote the two angles as angle X and angle Y. According to the definitions:
- If angle X and angle Y are supplementary, then:
X+Y=180∘
Step 3: Establish the Relationship of Vertically Opposite Angles
Since angle X and angle Y are also vertically opposite angles, we have:
- Vertically opposite angles are equal, so:
X=Y
Step 4: Substitute and Solve
Now, substituting Y with X in the supplementary angle equation:
X+X=180∘
This simplifies to:
2X=180∘
Dividing both sides by 2 gives:
X=90∘
Step 5: Conclusion
Since Y is equal to X, we also have:
Y=90∘
Thus, both angles are 90 degrees. Therefore, the angles which are both supplementary and vertically opposite are:
90∘ and 90∘
- Supplementary Angles: Two angles are supplementary if the sum of their measures is equal to 180 degrees.
- Vertically Opposite Angles: When two lines intersect, they form two pairs of opposite angles. These angles are called vertically opposite angles, and they are equal in measure.
Let’s denote the two angles as angle X and angle Y. According to the definitions:
- If angle X and angle Y are supplementary, then:
X+Y=180∘
Step 3: Establish the Relationship of Vertically Opposite Angles
Since angle X and angle Y are also vertically opposite angles, we have:
- Vertically opposite angles are equal, so:
X=Y
Now, substituting Y with X in the supplementary angle equation:
X+X=180∘
This simplifies to:
2X=180∘
Dividing both sides by 2 gives:
X=90∘
Since Y is equal to X, we also have:
Y=90∘
Thus, both angles are 90 degrees. Therefore, the angles which are both supplementary and vertically opposite are:
90∘ and 90∘
Topper's Solved these Questions
- LINES AND ANGLES BOOK - NCERT EXEMPLARCHAPTER - LINES AND ANGLES EXERCISE - Exercise (fill in the blanks)
3 Videos
- LINES AND ANGLES BOOK - NCERT EXEMPLARCHAPTER - LINES AND ANGLES EXERCISE - Think and Discuss
6 Videos
- INTEGERSBOOK - NCERT EXEMPLARCHAPTER - INTEGERSEXERCISE - VOCOBULARY
5 Videos
- PERIMETER AND AREABOOK - NCERT EXEMPLARCHAPTER - PERIMETER AND AREAEXERCISE - Think and Discuss
7 Videos
Similar Questions
Knowledge Check
Answer on the basis of the following statements. When two straight lines intersect, then :
adjacent angles are complementary
adjacent angles are supplementary
opposite angles are equal
opposite angles are supplementaryA2 and 3 are correctB1 and 4 are correctC1 and 3 are correctD2 and 4 are correct
Prove that vertically opposite angles are equal.
View SolutionIn the adjoining figure:
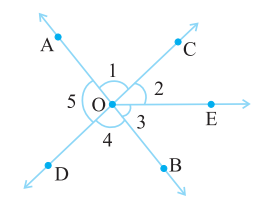
(i) Is ∠1 adjacent to ∠2? (ii) Is ∠AOC adjacent to ∠AOE?
(iii) Do ∠COE and ∠EOD form a linear pair?
(iv) Are ∠BOD and ∠DOA supplementary?
(v) Is ∠1 vertically opposite to ∠4?
(vi) What is the vertically opposite angle of ∠5?
View SolutionIndicate which pairs of angles are:
(i) Vertically opposite angles.
(ii) Linear pairs.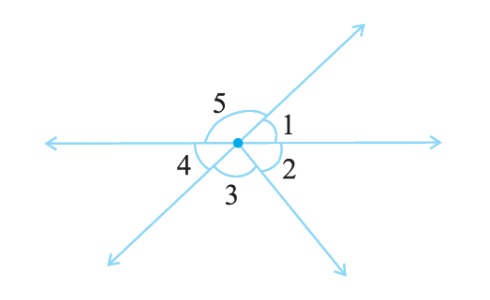
View SolutionThe angles are supplementary and larger is twice the smaller
View Solutionthe angles are supplementary and the smaller is one-half of the larger.
View SolutionThe measure of an angle is twice the measure of its supplementary angle. Find its measure.
View SolutionState whether the statements are True or False.
Vertically opposite angles are either both acute angles or both obtuse angles.
View Solution
