In Fig. 5.55, l ||m and a line t intersects these lines at P and Q, respectively. Find the sum 2a + b.
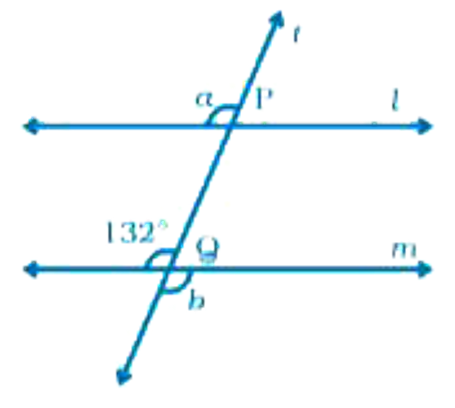
Step by step video & image solution for In Fig. 5.55, l ||m and a line t intersects these lines at P and Q, respectively. Find the sum 2a + b. by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
The lines L1:y−x=0 and L2:2x+y=0 intersect the line L3:y+2=0 at P and Q, respectively. The bisector of the acute angle between L1 and L2 intersects L3 at R.
Statement 1 : The ratio PR : RQ equals 2√2:√5.
Statement 2: In any triangle, bisector of an angle divides the triangle into two similar triangles.1AStatement 1 is true, statement 2 is false.BStatement 1 is true, statement 2 is true, statement 2 is the correct explanation of statement1.CStatement 1 is true, statement 2 is true, statement 2 is not the correct explanation of statement 1.DStatement 1 is false, statement 2 is true.
In Fig. l, m and n are parallel lines intersected by transversal p at X, Y and Z respectively. Find ∠1, ∠2 and ∠3
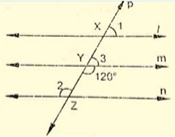
View SolutionIn Fig. 51, l, m and n are parallel lines intersected by a transversal p at X,Y and Z respectively. Find ∠1, ∠2 and ∠3. Give reasons.
View SolutionIn Fig. 4.238, S and T are points on the sides PQ and PR respectively of PQR such that PT=2cm , TR=4cm and ST is parallel to QR . Find the ratio of the areas of PST and PQR . (FIGURE)
View SolutionIn Figure, l,mandn are parallel lines intersected by a transversal at X,Y,andZ respectively. Find ∠1, ∠2 and∠3. Give reasons.
Let∠1=3xand∠2=2x
∠1+∠2=180∘
⇒5x=180∘
x=36∘
∠1=108∘,∠2=72∘
Since m∥nand l is the intersector
∠3=∠1=108∘ and ∠4=∠2=72∘ (Opposite angles
∠7=∠5=∠2=72∘
=∠5=72∘
∠6=108∘=∠8
View SolutionIn Fig. 60, AB and CD are parallel lines intersected by a transversal PQ at L and M respectively. If ∠LMD=350 find ∠PLA.
View SolutionLet a given line L1 intersect the X and Y axes at P and Q respectively. Let another line L2 perpendicular to L1 cut the X and Y-axes at Rand S, respectively. Show that the locus of the point of intersection of the line PS and QR is a circle passing through the origin
View SolutionTwo circles intersect at two points B and C. Through B, two line segments ABD and PBQ are drawn to intersect the circles at A, D and P, Q respectively (see Fig. 10.40). Prove that ∠ACP =∠QCD.
View Solution