IfΔPQRandΔXYZare congruent under the correspondence QPR↔XYZ, then
∠R=…….
To find the measurement of angle R in the congruent triangles ∆PQR and ∆XYZ, we can follow these steps:
1. Understand the Congruence: Since ∆PQR and ∆XYZ are congruent under the correspondence QPR ↔ XYZ, we know that the corresponding angles and sides of the triangles are equal.
Hint: Remember that congruent triangles have equal corresponding angles and sides.
2. Identify Corresponding Angles: From the given correspondence:
- Angle Q corresponds to Angle X
- Angle R corresponds to Angle Z
- Angle P corresponds to Angle Y
Hint: Write down the pairs of corresponding angles to avoid confusion.
3. Write the Equality of Angles: Based on the correspondence:
- Angle R = Angle Z
Hint: Use the congruence property to establish relationships between angles.
4. Conclusion: Therefore, we can conclude that:
- Angle R = Angle Z
Hint: Make sure to state the final answer clearly.
Final Answer:
Angle R = Angle Z
- Angle Q corresponds to Angle X
- Angle R corresponds to Angle Z
- Angle P corresponds to Angle Y
- Angle R = Angle Z
- Angle R = Angle Z
Angle R = Angle Z
Topper's Solved these Questions
Similar Questions
For △PQR and △XYZ, the correspondence PQR↔YZX is a similarity, m∠P=2m∠Q and m∠X=120. Find m∠Y.
View SolutionIn a ΔPQR as show in figure given that x:y:z::2:3:6, then find value of ∠QPR.
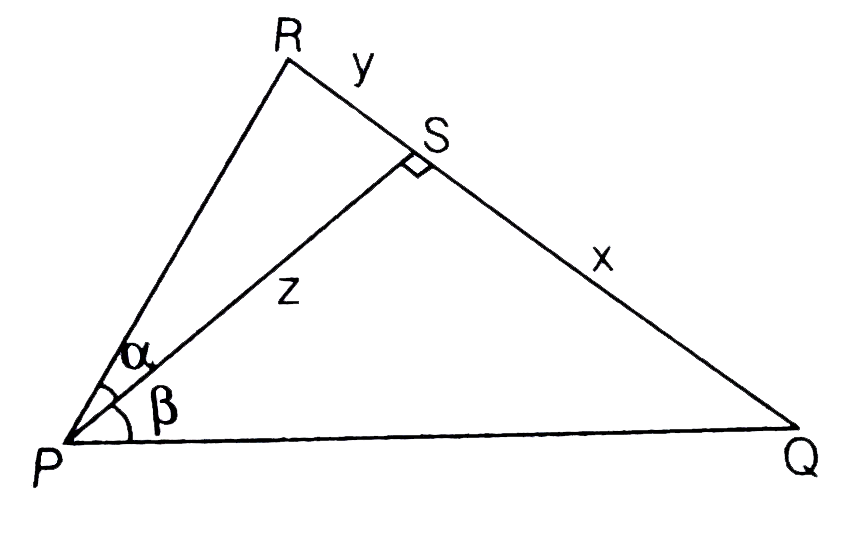
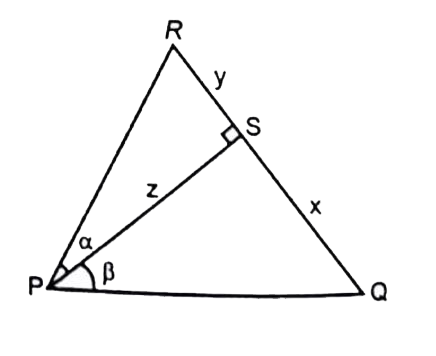
View SolutionIn a ΔPQR (as shown in figure) if x:y:z=2:3:6, then the value of ∠QPR is :
View SolutionIf in triangles PQR and XYZ PQXZ=PRXY=QRYZ, then :
View SolutionState the correspondence between the vertices, sides and angles of the following pairs of congruent triangles.
Q (i) △ABC=△EFD
(ii) △CAB=△QRP
(iii) (i) △XYZ=△QPR
(iv)(i) △MPN=△SQR
View SolutionWrite the coefficient of: (i)z in −7xyz (ii) p in −3pqr
View SolutionIf in triangles PQR and XYZ ; PQXZ=PRXY=QRYZ then:
View Solution