Rectangular prism and cuboid refer to the same solid.
To determine whether the statement "Rectangular prism and cuboid refer to the same solid" is right or wrong, we can analyze the definitions and properties of both shapes step by step.
1. Definition of Rectangular Prism:
A rectangular prism is a three-dimensional shape that has six faces, all of which are rectangles. It has a length, width, and height.
Hint: Remember that a rectangular prism is defined by its rectangular faces.
2. Definition of Cuboid:
A cuboid is also a three-dimensional shape that has six faces, where each face is a rectangle. In fact, a cuboid can be defined as a rectangular prism.
Hint: Consider that a cuboid is a specific type of rectangular prism.
3. Properties of Both Shapes:
- Both shapes have 6 faces, 12 edges, and 8 vertices.
- The faces of both shapes are rectangles.
Hint: Compare the properties of both shapes to see if they match.
4. Conclusion:
Since both the rectangular prism and cuboid have the same properties and definitions, we can conclude that they refer to the same solid.
Hint: Think about whether the definitions and properties align to determine if they are the same.
Final Answer:
The statement "Rectangular prism and cuboid refer to the same solid" is correct.
A rectangular prism is a three-dimensional shape that has six faces, all of which are rectangles. It has a length, width, and height.
A cuboid is also a three-dimensional shape that has six faces, where each face is a rectangle. In fact, a cuboid can be defined as a rectangular prism.
- Both shapes have 6 faces, 12 edges, and 8 vertices.
- The faces of both shapes are rectangles.
Since both the rectangular prism and cuboid have the same properties and definitions, we can conclude that they refer to the same solid.
The statement "Rectangular prism and cuboid refer to the same solid" is correct.
Topper's Solved these Questions
- PRACTICAL GEOMETRY SYMMETRY AND VISUALISING SOLID SHAPESBOOK - NCERT EXEMPLARCHAPTER - PRACTICAL GEOMETRY SYMMETRY AND VISUALISING SOLID SHAPESEXERCISE - THINK AND DISCUSS
6 Videos
- PERIMETER AND AREABOOK - NCERT EXEMPLARCHAPTER - PERIMETER AND AREAEXERCISE - Think and Discuss
7 Videos
- RATIONAL NUMBERSBOOK - NCERT EXEMPLARCHAPTER - RATIONAL NUMBERSEXERCISE - Application
2 Videos
Similar Questions
Knowledge Check
If the base of right rectangular prism remains constant and the measures of the lateral edges are halved, then its volume will be redeuced by :
A50%B33.33%C66.66%Dnone of theseIf the base of right rectangular prism remains constant and the measures of the lateral edges are halved, then its volume will be redeuced by :
A50%B33.33%C66.66%Dnone of theseA convex lens, a glass slab, a glass prism and a solid sphere all are made of the same glass, the dispersive power will be
AIn the glass slab and prismBIn the lens and solid sphereCOnly in prismDIn all the four
The net of a rectangular prism has ______ rectangles.
View SolutionA rectangular prism is made by joining some cubes as shown in the given figure. The volume of each small cube is 1 cm3.
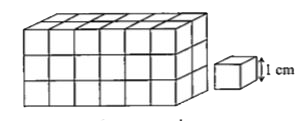
The volume of a rectangular prism is
View SolutionThe area of a square park is the same as of a rectangular park. If the side of the square park is 60 m and the length of the rectangular park is 90 m, find the breadth of the rectangular park.
View SolutionRectangular prism is also called a ________.
View SolutionFaces Fig. 16.1 is made of six rectangular plane regions namely ABCDEFGH CGFB AEFB and CDHG. These six rectangular plane regions are six faces of the cuboid shown in Fig. 16. 1.
View Solution