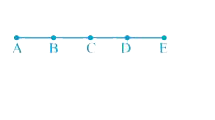
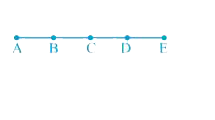
In Fig. 2.15, points A,B,C,D and E are collinear such that AB = BC = CD= DE. Then
AE = ________ × AB.
Step by step video & image solution for In Fig. 2.15, points A,B,C,D and E are collinear such that AB = BC = CD= DE. Then AE = ________ xx AB. by Maths experts to help you in doubts & scoring excellent marks in Class 6 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GEOMETRYBOOK - NCERT EXEMPLARCHAPTER - GEOMETRYEXERCISE - Exercise (State whether the statements given in questions are true (T) or false (F):)
10 Videos
- GEOMETRYBOOK - NCERT EXEMPLARCHAPTER - GEOMETRYEXERCISE - Exercise
56 Videos
- GEOMETRYBOOK - NCERT EXEMPLARCHAPTER - GEOMETRYEXERCISE - Exercise (Out of foure options only one is correct. Write the correct answer.)
16 Videos
- FRACTIONS AND DECIMALS BOOK - NCERT EXEMPLARCHAPTER - FRACTIONS AND DECIMALS EXERCISE - ACTIVITY
1 Videos
- INTEGERS BOOK - NCERT EXEMPLARCHAPTER - INTEGERS EXERCISE - Exercise
42 Videos
Similar Questions
Knowledge Check
A sum of money lent at compound interest for 2 years at 20% per annum would fetch Rs 482 more, if the interest was payable half-yearly than if it was payable annually. The sum is: (a) Rs 10,000 (b) Rs 20,000 (c) Rs 40,000 (d) Rs 50,000
AA. 30000BB. 20000CC. 10000DD.50000For a triangle ABC,D and E are two points on AB and AC such that AD=14AB,AE=14AC. If BC=12cm, then DE is
Aa) 5 cmBb) 4 cmCc) 3 cmDd) 6 cm
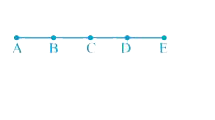
In Fig. 2.15, points A,B,C,D and E are collinear such that AB = BC = CD= DE. Then
mid point of AE is __________
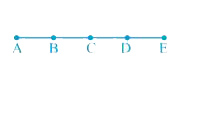
View SolutionIn Fig. 2.15, points A,B,C,D and E are collinear such that AB = BC = CD= DE. Then
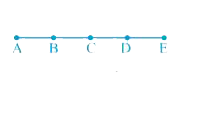
mid point of CE is __________
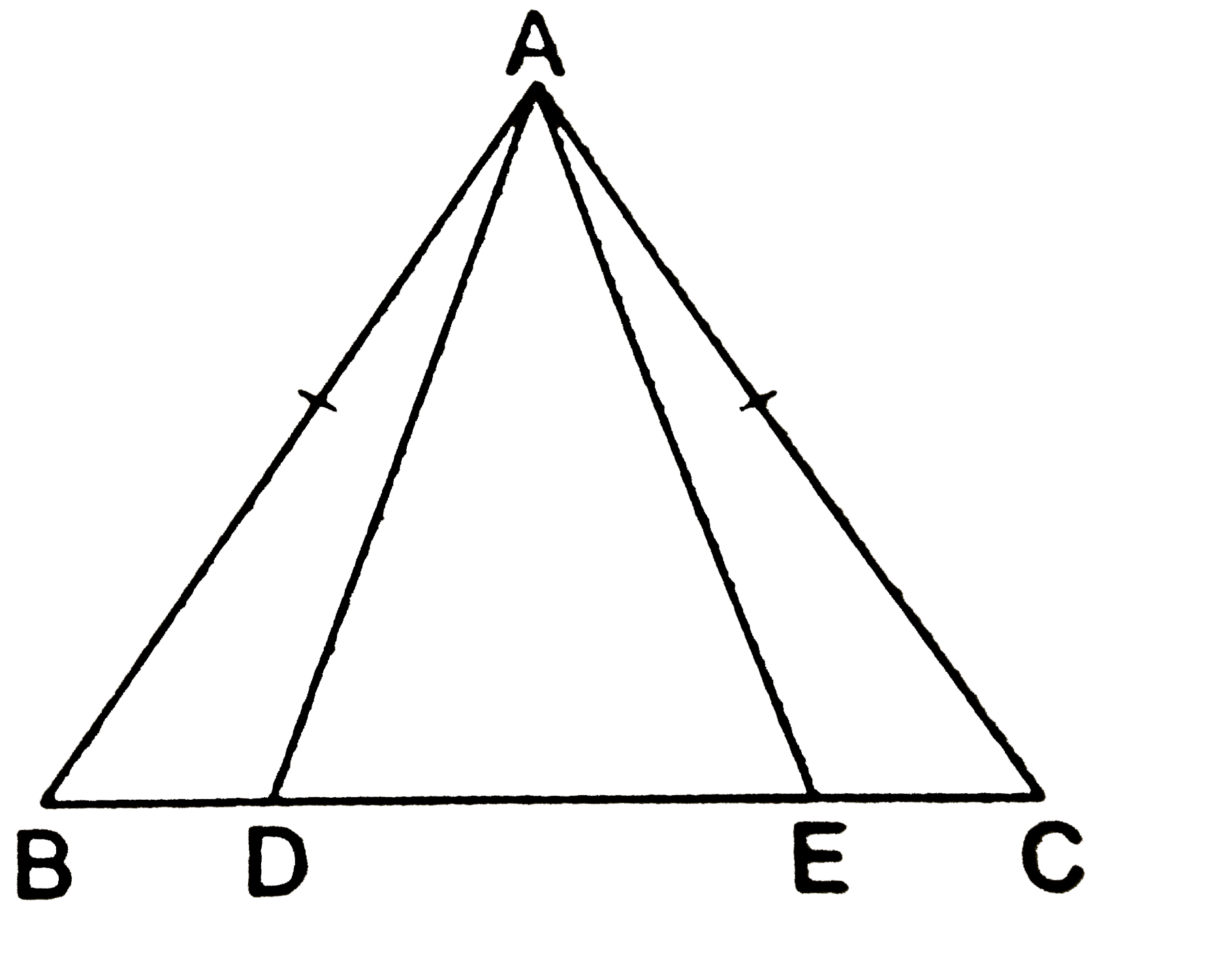
View SolutionIn an isosceles ΔABC with AB = AC, D and E are point on BC such that BE = CD. Show that AD = AE.
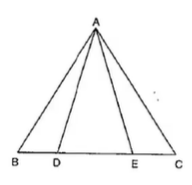
View SolutionIn Figure, AD=AE and D and E are points on BC such that BD=EC. Prove that AB=AC
View SolutionLet A, B, C, D be points on a vertical line such that AB = BC = CD. If a body is released from position A, the times of descent through AB, BC and CD are in the ratio.
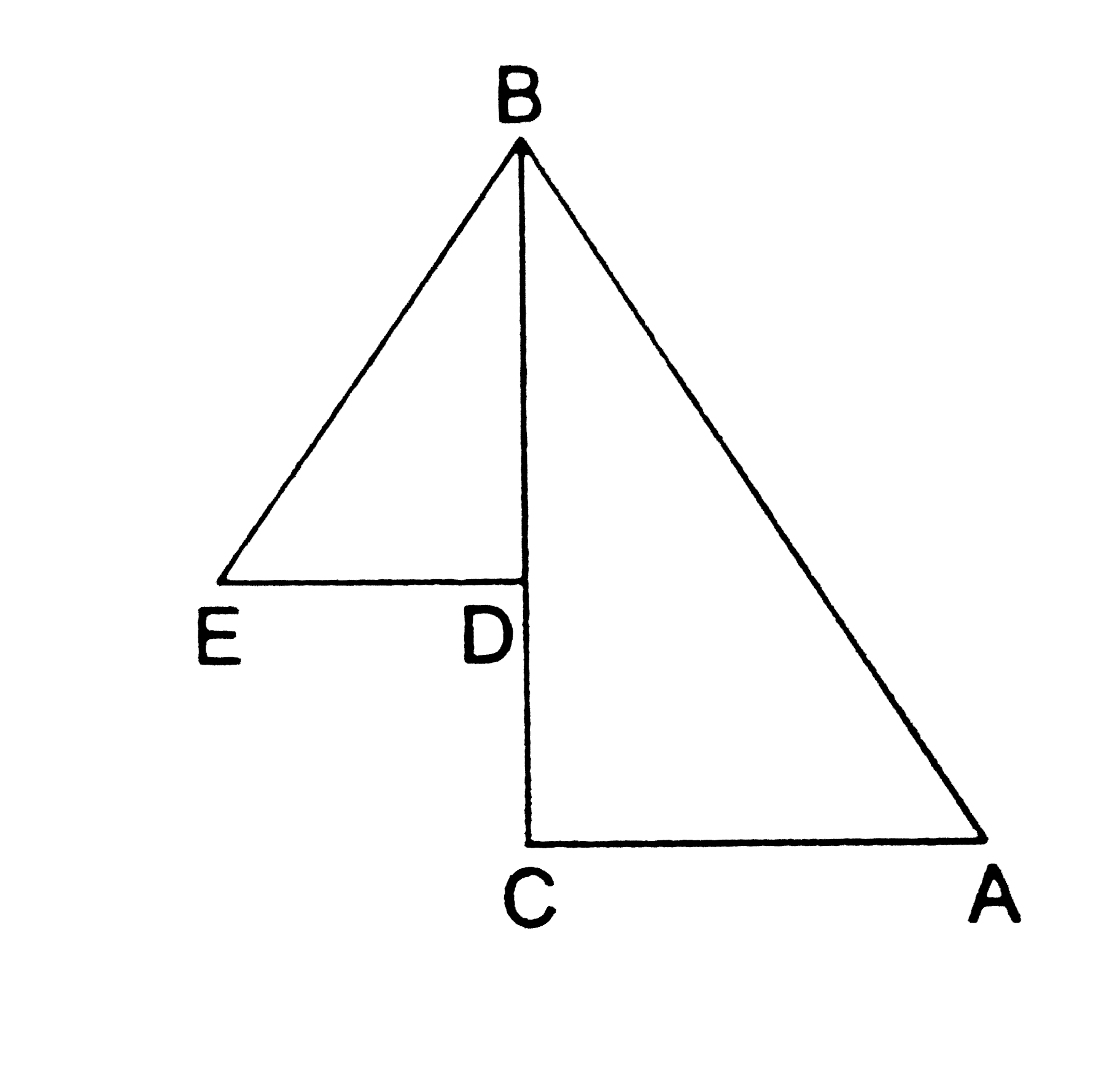
View SolutionIn the given figure, D is a point on side BC of a ΔABC and E is a point such that CD = DE.
Prove that AB+AC>BE.
View Solution