A rectangle is divided into certain number of equal parts. If 16 of the parts so formed represent the fraction 14, find the number of parts in which the rectangle has been divided.
To solve the problem step by step, we need to find out how many total parts the rectangle has been divided into, given that 16 parts represent the fraction 14.
Step 1: Understand the relationship between parts and fractions
The problem states that 16 parts represent 14 of the total parts. This means that if 16 parts are 14, then the total number of parts can be found by determining how many times 14 fits into 1 (the whole).
Hint: Remember that if a certain number of parts represents a fraction of the whole, you can find the total by using the relationship between the fraction and the total.
Step 2: Set up the equation
Let x be the total number of parts in the rectangle. Since 16 parts represent 14, we can write the equation:
14×x=16
Hint: Think about how fractions work: if 14 of something equals a certain number, you can multiply that number by the denominator of the fraction to find the total.
Step 3: Solve for x
To find x, we can rearrange the equation:
x=16×4
Now, calculate 16×4:
x=64
Hint: When multiplying, you can break it down into smaller parts if needed. For example, 16×4 can also be thought of as 16×(2+2).
Step 4: Conclusion
The total number of parts in which the rectangle has been divided is 64.
Final Answer: The rectangle has been divided into 64 parts.
The problem states that 16 parts represent 14 of the total parts. This means that if 16 parts are 14, then the total number of parts can be found by determining how many times 14 fits into 1 (the whole).
Let x be the total number of parts in the rectangle. Since 16 parts represent 14, we can write the equation:
14×x=16
To find x, we can rearrange the equation:
x=16×4
x=64
The total number of parts in which the rectangle has been divided is 64.
Topper's Solved these Questions
- FRACTIONS AND DECIMALS BOOK - NCERT EXEMPLARCHAPTER - FRACTIONS AND DECIMALS EXERCISE - ACTIVITY
1 Videos
- FRACTIONS AND DECIMALS BOOK - NCERT EXEMPLARCHAPTER - FRACTIONS AND DECIMALS EXERCISE - EXERCISE (TRUE OR FALSE )
21 Videos
- DATA HANDLINGBOOK - NCERT EXEMPLARCHAPTER - DATA HANDLINGEXERCISE - Exercise
66 Videos
- GEOMETRYBOOK - NCERT EXEMPLARCHAPTER - GEOMETRYEXERCISE - Exercise
56 Videos
Similar Questions
Knowledge Check
The parts into which the earth's lithosphere is divided is
Afault plateBtectonic platesCepicentreDcoreThe capital of a company is divided into number of parts , each one of which is called
ADividendBProfitCInterestDShareNumber of sub parts into which ‘n’ straight lines in a plane can divide it is:
An2+n+22Bn2+n+42Cn2+n+62Dnone
The number of ways in which 4n things can be divided into 4 equal parts is
View SolutionPercentilies divide the series into ____________ equal parts.
View SolutionDivide 29 into two parts so that the sum of the squares of the parts is 425.
View SolutionIn percentilies , series is divided in hundred equal parts.
View SolutionA rectangle is divided into 16 sub-rectangles as in the figure, the number in each sub rectangle represents the are of that sub-rectangle. What is the area of the rectangle KLMS ?
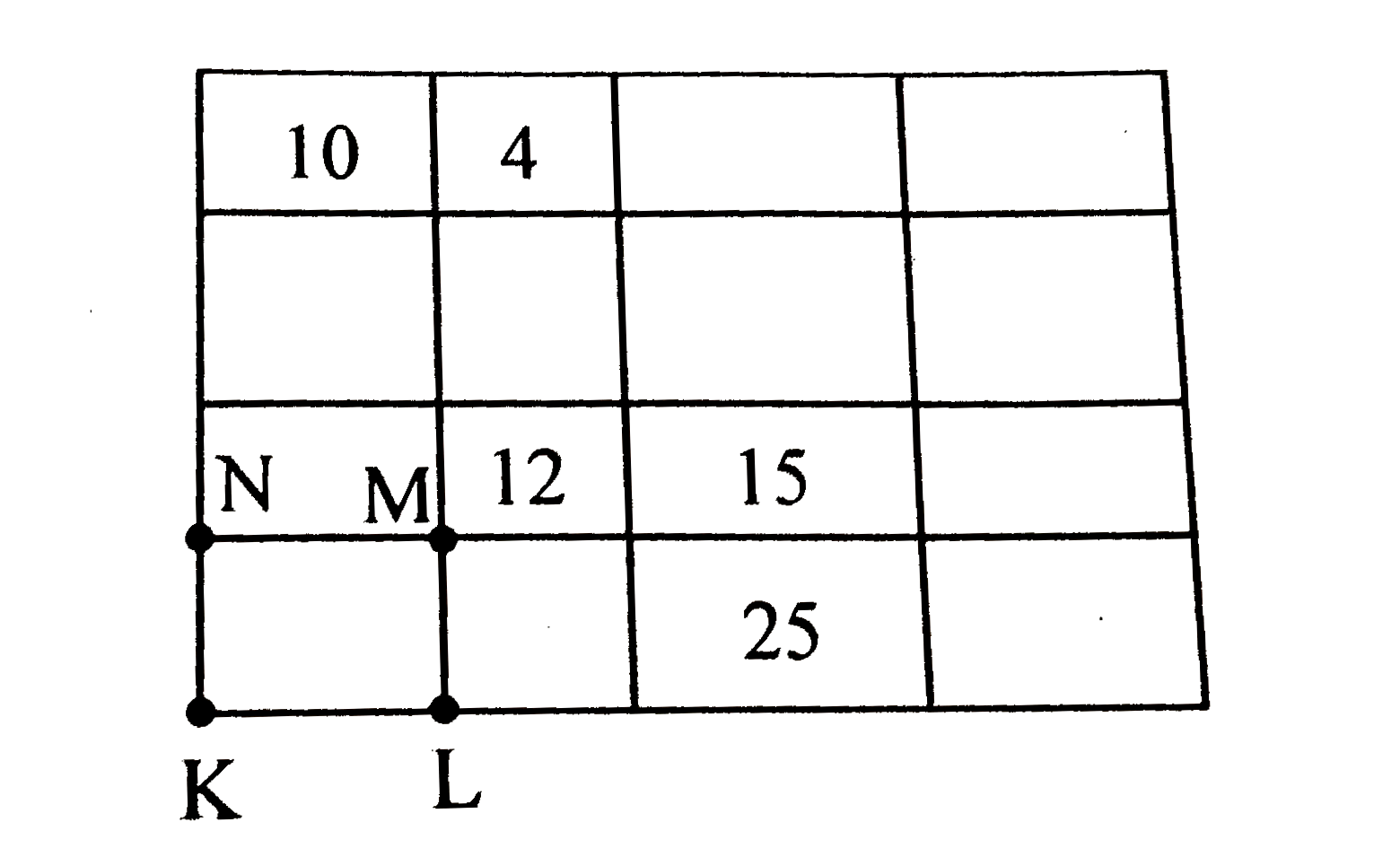
View Solution
