The lawn in front of Molly's house is 12m×8m, whereas the lawn in front of Dolly's house is 15m×5m. A bamboo fencing is built around both the lawns. How much fencing is required for both?
To find the total length of fencing required for both lawns, we need to calculate the perimeter of each lawn separately and then add them together.
Step 1: Calculate the perimeter of Molly's lawn.
- The dimensions of Molly's lawn are given as 12 m (length) and 8 m (breadth).
- The formula for the perimeter (P) of a rectangle is:
P=2×(length+breadth)
- Substituting the values:
P=2×(12m+8m)=2×20m=40m
Step 2: Calculate the perimeter of Dolly's lawn.
- The dimensions of Dolly's lawn are given as 15 m (length) and 5 m (breadth).
- Using the same perimeter formula:
P=2×(length+breadth)
- Substituting the values:
P=2×(15m+5m)=2×20m=40m
Step 3: Calculate the total length of fencing required.
- Now, we add the perimeters of both lawns:
Total fencing=Perimeter of Molly's lawn+Perimeter of Dolly's lawn
- Substituting the values:
Total fencing=40m+40m=80m
Final Answer:
The total length of fencing required for both lawns is 80 meters.
---
- The dimensions of Molly's lawn are given as 12 m (length) and 8 m (breadth).
- The formula for the perimeter (P) of a rectangle is:
P=2×(length+breadth)
- Substituting the values:
P=2×(12m+8m)=2×20m=40m
- The dimensions of Dolly's lawn are given as 15 m (length) and 5 m (breadth).
- Using the same perimeter formula:
P=2×(length+breadth)
- Substituting the values:
P=2×(15m+5m)=2×20m=40m
- Now, we add the perimeters of both lawns:
Total fencing=Perimeter of Molly's lawn+Perimeter of Dolly's lawn
- Substituting the values:
Total fencing=40m+40m=80m
The total length of fencing required for both lawns is 80 meters.
Topper's Solved these Questions
- MENSURATIONBOOK - NCERT EXEMPLARCHAPTER - MENSURATIONEXERCISE - Exercise (Fill in the blanks)
5 Videos
- MENSURATIONBOOK - NCERT EXEMPLARCHAPTER - MENSURATIONEXERCISE - Exercise (True or False)
7 Videos
- MENSURATIONBOOK - NCERT EXEMPLARCHAPTER - MENSURATIONEXERCISE - Exercise (Multiple Choice Questions)
6 Videos
- INTEGERS BOOK - NCERT EXEMPLARCHAPTER - INTEGERS EXERCISE - Exercise
42 Videos
- NUMBER SYSTEMBOOK - NCERT EXEMPLARCHAPTER - NUMBER SYSTEMEXERCISE - Exercise
49 Videos
Similar Questions
Knowledge Check
The mean radius of the earth's orbit around the sun is 1.5×1011m and that of the orbit of mercury is 6×1010m. The mercury will revolve around the sun is nearly
A√25yrB25yrC(25)2yrD(25)3/2yr
Hari and Vamshi constructed houses adjacent to each other, in such a way that the ground floors of both the houses are of height 1 m each from the level or the road. Vamshi built an inclined plane in front of his house so that its length is 50% more than of Hari's house Find the ratio of hte efforts required to lift the same load to the ground floor of both houses
View SolutionA lawn is in the form of a rectangle whose sides are in the ratio 5:3 the area of the lawn is 3375 m2 .Find the cost of fencing the lawn at Rs. 65 per metre.
View SolutionA closed cylindrical tank of radius 1.5m and height 3m is made from a sheet of metal. How much sheet of metal is required?
View SolutionA square lawn is of side 110m. A road 5 m is made all around inside the lawn. Find the area of the road in km2
View SolutionA lawn is in the form of a rectangle whose sides are in the ratio 5:3 and its area is 3375 m2.Find the cost of fencing the lawn at Rs. 20 per metre .
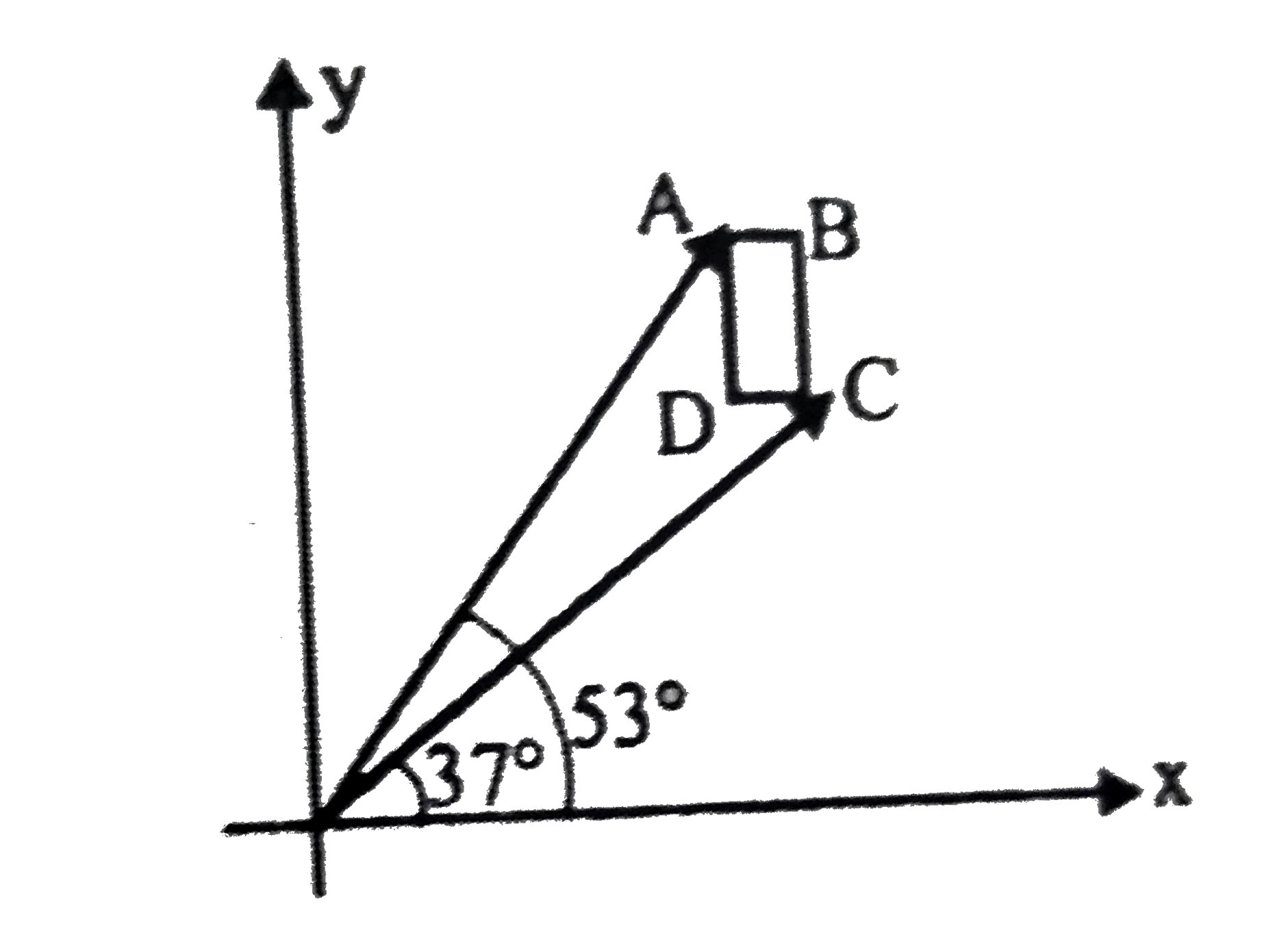
View SolutionThe farm house shown in figure has rectangular shape and has sides parallel to the chosen x and y axes. The position vector of corner A is 125 m at 53∘ and corner C is 100 m at 37∘ from x axis. Find the length of the fencing required in meter.
View SolutionThe dimensions of a room are (10 m x 8m x 3.3 m). How many men can be accommodated in this room if each man required 3m3 of space
View Solution
