State True or False:
To determine whether the statement 27 cm² : 57 cm² = 18 cm : 38 cm is true or false, we will simplify both ratios and compare them.
Step 1: Simplify the first ratio (27 cm² : 57 cm²)
The first ratio can be expressed as a fraction:
\(
\frac{27 \text{ cm}^2}{57 \text{ cm}^2}
\)
Step 2: Simplify the fraction
To simplify \(\frac{27}{57}\), we can find the greatest common divisor (GCD) of 27 and 57.
- The factors of 27 are: 1, 3, 9, 27
- The factors of 57 are: 1, 3, 19, 57
The GCD is 3. Now, we divide both the numerator and the denominator by 3:
\(
\frac{27 \div 3}{57 \div 3} = \frac{9}{19}
\)
Thus, the first ratio simplifies to:
\(
27 \text{ cm}^2 : 57 \text{ cm}^2 = 9 : 19
\)
Step 3: Simplify the second ratio (18 cm : 38 cm)
Now, we simplify the second ratio:
\(
\frac{18 \text{ cm}}{38 \text{ cm}}
\)
Step 4: Simplify the fraction
To simplify \(\frac{18}{38}\), we find the GCD of 18 and 38.
- The factors of 18 are: 1, 2, 3, 6, 9, 18
- The factors of 38 are: 1, 2, 19, 38
The GCD is 2. Now, we divide both the numerator and the denominator by 2:
\(
\frac{18 \div 2}{38 \div 2} = \frac{9}{19}
\)
Thus, the second ratio simplifies to:
\(
18 \text{ cm} : 38 \text{ cm} = 9 : 19
\)
Step 5: Compare the two simplified ratios
Now we compare the two simplified ratios:
- First ratio: \(9 : 19\)
- Second ratio: \(9 : 19\)
Since both ratios are equal, we conclude that the statement is true.
Final Answer:
The statement 27cm²:57cm²=18cm:38cm is True.
---
\(
\frac{27 \text{ cm}^2}{57 \text{ cm}^2}
\)
- The factors of 57 are: 1, 3, 19, 57
\(
\frac{27 \div 3}{57 \div 3} = \frac{9}{19}
\)
\(
27 \text{ cm}^2 : 57 \text{ cm}^2 = 9 : 19
\)
\(
\frac{18 \text{ cm}}{38 \text{ cm}}
\)
- The factors of 38 are: 1, 2, 19, 38
\(
\frac{18 \div 2}{38 \div 2} = \frac{9}{19}
\)
\(
18 \text{ cm} : 38 \text{ cm} = 9 : 19
\)
- First ratio: \(9 : 19\)
- Second ratio: \(9 : 19\)
The statement 27cm²:57cm²=18cm:38cm is True.
Topper's Solved these Questions
- RATIO AND PROPORTIONBook:NCERT EXEMPLARChapter:RATIO AND PROPORTIONExercise: Exercise (In questions 16 to 34, state whether the given statements are true (T) or false (F).
Explore 1 Video
- RATIO AND PROPORTIONBook:NCERT EXEMPLARChapter:RATIO AND PROPORTIONExercise: Exercise (In questions 35 to 46, fill in the blanks to make the statements true.)
Explore 11 Videos
- RATIO AND PROPORTIONBook:NCERT EXEMPLARChapter:RATIO AND PROPORTIONExercise: Exercise
Explore 70 Videos
- NUMBER SYSTEMBook:NCERT EXEMPLARChapter:NUMBER SYSTEMExercise:Exercise
Explore 49 Videos
- SYMMETRY AND PRACTICAL GEOMETRY Book:NCERT EXEMPLARChapter:SYMMETRY AND PRACTICAL GEOMETRY Exercise:Exercise
Explore 29 Videos
Similar Questions
The length, width and height of a rectangular solid are in the ratio of 3:2:1. If the volume of the box is 48 cm3, the total surface area of the box is: (a) 27 cm2 (b) 32 cm2 (c) 44 cm2 (d) 88 cm2
View SolutionState True or False
Triangle with length of sides as 5 cm, 6 cm and 11 cm can be constructed.
View SolutionThe base of triangle is 15 cm and height is 12 cm. The height of another triangle of double the area having base 20cm is (a) 22 cm (b) 20 cm (c) 18 cm (d) 10 cm
View SolutionThe perimeter of an isosceles right-angled triangle having an area of 162cm2 is (a) 40 cm (b) 56.5 cm (c) 61.38 cm (d) 68.2 cm
View Solution40. For each of the following figures, find What is the distance to travel in a round The tur Does it happen? 8 cm __7 cm 8 cm 7 cm (1) 64 cm (3) 40 cm 8 cm (2) 22 cm (4) 38 cm
View SolutionThe radius of the base and height of a metallic solid cylinder are r cm and 6 cm respectively. It is melted and recast into a solid cone of the same radius of base. The height of the cone is (a) 9 cm (b) 18 cm (c) 27 cm (d) 54 cm
View SolutionConvert 46m18cm to cm
View SolutionM and N are points on sides AC and BC respectively of a △ABC. State whether MN||BC if CM = 4.2 cm, MA= 2.8 cm , NB = 3.6 cm, CN = 5.7 cm.
View SolutionThe diameter of a circle is 3.5 cm. What is the circumference of the circle? (a) 11 cm (b) 22 cm (c) 38.5 cm (d) 45.2 cm (e) None of these
View SolutionIn the figure ∠ADC=90∘,BC=38cm,CD=28cmandBP=25cm
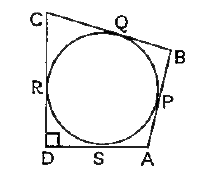
Find the radius of the circle.
View Solution
