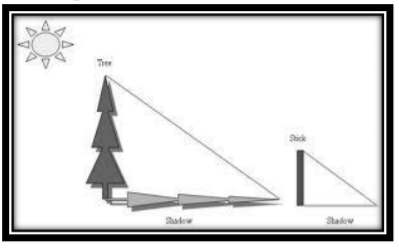
The shadow of a 3m long stick is 4m long. At the same time of the day, if the shadow of a flagstaff is 24m long, how tall is the flagstaff?
To solve the problem, we will use the concept of ratios and proportions.
1. Identify the known values:
- The height of the stick = 3 meters
- The length of the stick's shadow = 4 meters
- The length of the flagstaff's shadow = 24 meters
- We need to find the height of the flagstaff, which we will denote as X.
2. Set up the proportion:
Since the stick and the flagstaff cast shadows at the same time of day, we can set up a proportion based on their heights and shadow lengths:
Height of the stickLength of the stick's shadow=Height of the flagstaffLength of the flagstaff's shadow
This translates to:
34=X24
3. Cross-multiply to solve for X:
Cross-multiplying gives us:
3×24=4×X
This simplifies to:
72=4X
4. Isolate X:
To find X, divide both sides of the equation by 4:
X=724
Simplifying this gives:
X=18
5. Conclusion:
The height of the flagstaff is 18 meters.
- The height of the stick = 3 meters
- The length of the stick's shadow = 4 meters
- The length of the flagstaff's shadow = 24 meters
- We need to find the height of the flagstaff, which we will denote as X.
Since the stick and the flagstaff cast shadows at the same time of day, we can set up a proportion based on their heights and shadow lengths:
Height of the stickLength of the stick's shadow=Height of the flagstaffLength of the flagstaff's shadow
This translates to:
34=X24
Cross-multiplying gives us:
3×24=4×X
This simplifies to:
72=4X
To find X, divide both sides of the equation by 4:
X=724
Simplifying this gives:
X=18
The height of the flagstaff is 18 meters.
Topper's Solved these Questions
- RATIO AND PROPORTIONBOOK - NCERT EXEMPLARCHAPTER - RATIO AND PROPORTIONEXERCISE - Exercise (In questions 16 to 34, state whether the given statements are true (T) or false (F). )
18 Videos
- RATIO AND PROPORTIONBOOK - NCERT EXEMPLARCHAPTER - RATIO AND PROPORTIONEXERCISE - Exercise (In questions 16 to 34, state whether the given statements are true (T) or false (F).
1 Videos
- RATIO AND PROPORTIONBOOK - NCERT EXEMPLARCHAPTER - RATIO AND PROPORTIONEXERCISE - Exercise (In questions 35 to 46, fill in the blanks to make the statements true.)
11 Videos
- NUMBER SYSTEMBOOK - NCERT EXEMPLARCHAPTER - NUMBER SYSTEMEXERCISE - Exercise
49 Videos
- SYMMETRY AND PRACTICAL GEOMETRY BOOK - NCERT EXEMPLARCHAPTER - SYMMETRY AND PRACTICAL GEOMETRY EXERCISE - Exercise
29 Videos
Similar Questions
Knowledge Check
The shadow of a 5-m-long stick is 2m long. At the same time, the length of the shadow of a 12.5m high tree is
A3mB3.5mC4.5mD5mThe shadow of a flagstaff is three times as long as the shadow of the flagstaff when the sun rays meet the ground at 60∘ . Find the angle between the sun rays and the ground at the time of longer shadow
A45∘B30∘C15∘D90∘At a particular time , the shadow cast by a tower is 6 m long. If the distance from the top of the tower to the end of the shadow is 10 m long, determine the height of the tower.
A4 mB8 mC16 mD12 m
X is 5 m tall and he notices that he casts a shadow that is 3 m long. He then measures that the shadow cast by his school building is 30 m long. How tall is the building?
View SolutionA tree 6 m tall casts a shadow 4m long. At the same time if a tower casts the shadow 10m long then find the height of the tower.
View SolutionA man 6 ft tall casts a shadow 4 ft long , at the same time when a flag pole casts a shadow 50 ft long .The height of the flag pole is
View SolutionQuestion Stimulus :-
An apartment casts a shadow of length 654 m long and at the same time a tree standing in front of it casts a shadow of length 6 meters. If the tree is 2 m of height, what is the height of the apartment?
View SolutionA tree is 12m tall and casts an 8 m long shadow. At the same time, a flag pole casts a 100m long shadow. How long is the flag pole?
View Solution

 (i)3m
(i)3m