Draw the images P' , Q' and R' of the point P, Q and R respectively in the line n (Fig . 9. 18). Join P' Q' and Q' R' to form an angle P' Q' R' Measure ∠PQRand∠P'Q'R' . Are the two angles equal ?
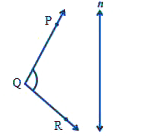
Step by step video & image solution for Draw the images P' , Q' and R' of the point P, Q and R respectively in the line n (Fig . 9. 18). Join P' Q' and Q' R' to form an angle P' Q' R' Measure angle PQR and angle P' Q' R' . Are the two angles equal ? by Maths experts to help you in doubts & scoring excellent marks in Class 6 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SYMMETRY AND PRACTICAL GEOMETRY BOOK - NCERT EXEMPLARCHAPTER - SYMMETRY AND PRACTICAL GEOMETRY EXERCISE - Exercise (In questions 43 - 61, state whether the statements are true (T) or false (F).)
19 Videos
- RATIO AND PROPORTIONBOOK - NCERT EXEMPLARCHAPTER - RATIO AND PROPORTIONEXERCISE - Exercise (In questions 35 to 46, fill in the blanks to make the statements true.)
11 Videos
Similar Questions
Knowledge Check
In a parallelogram PQRS, angle P is four times of angle Q, then the measure of ∠R is
A144∘B36∘C72∘D130∘In ΔPQR,∠P:∠Q:∠R=1:3:5. What is the value of (in degress) of ∠R−∠P?
A30B80C45D60Two particles p and q located at distances rp and rq respectively from the centre of a rotating disc such that rp>rq.
Aboth p and q have the same accelerationBboth p and q do not have any accelerationCp has greater acceleration then qDq has greater acceleration than p
Two forces P and Q act at such an angle that R=P. If P is doubled, the new resultant is at right angles to Q.
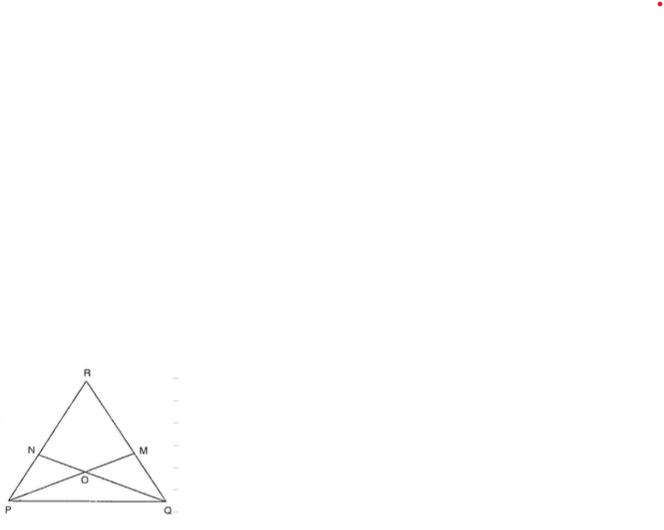
View SolutionIn Figure, ∠QPR=∠PQR and M and N are respectively on sides QR and PR of PQR such that QM=PN . Prove that OP=OQ, where O is the point of intersection of PM and QN.
View SolutionIn the formula ∠P+∠Q+∠R+∠S=360∘, if ∠P=100∘,∠Q=100∘, and ∠R=100∘, then find ∠S.
View SolutionGiven that P 12, Q = 5 and R = 13 also P+Q=R, then the angle between P and Q will be
View SolutionIf p, q and r are perpendicular to q + r, r + p and p + q respectively and if |p + q| = 6, |q + r| = 4√3 and |r + p| = 4, then |p + q + r| is
View Solution
