In the formula V=Ebda, if V , E and d are the velocity of longitudinal waves, bulk modulus of elasticity and density of the gaseous medium respectively, then the values of a and b are respectively.
−12and12
12and−12
−1√2and1√2
−1√2and−1√2
The correct Answer is:A
To solve the problem given by the formula V=Ebda, where V is the velocity of longitudinal waves, E is the bulk modulus of elasticity, and d is the density of the gaseous medium, we need to find the values of a and b.
Step 1: Write the dimensions of each variable
- Velocity (V): The dimension of velocity is given by:
(V)=LT−1
- Bulk Modulus of Elasticity (E): The bulk modulus is defined as stress divided by strain. Since strain is dimensionless, we have:
(E)=ForceArea=MLT−2L2=ML−1T−2
- Density (d): The density is mass per unit volume:
(d)=ML3=ML−3
Step 2: Substitute the dimensions into the equation
The equation V=Ebda can be expressed in terms of dimensions:
(LT−1)=(E)b(d)a
Substituting the dimensions we found:
LT−1=(ML−1T−2)b(ML−3)a
Step 3: Expand the right-hand side
Expanding the right-hand side:
LT−1=MbL−bT−2b⋅MaL−3a=Mb+aL−b−3aT−2b
Step 4: Equate the dimensions
Now, we equate the dimensions on both sides:
1. For mass (M):
0=b+a(1)
2. For length (L):
1=−b−3a(2)
3. For time (T):
−1=−2b(3)
Step 5: Solve the equations
From equation (3):
−1=−2b⟹b=12
Substituting b=12 into equation (1):
0=12+a⟹a=−12
Conclusion
Thus, the values of a and b are:
a=−12,b=12
Final Answer
The values of a and b are respectively −12 and 12.
- Velocity (V): The dimension of velocity is given by:
(V)=LT−1
- Bulk Modulus of Elasticity (E): The bulk modulus is defined as stress divided by strain. Since strain is dimensionless, we have:
(E)=ForceArea=MLT−2L2=ML−1T−2
- Density (d): The density is mass per unit volume:
(d)=ML3=ML−3
The equation V=Ebda can be expressed in terms of dimensions:
(LT−1)=(E)b(d)a
Substituting the dimensions we found:
LT−1=(ML−1T−2)b(ML−3)a
Expanding the right-hand side:
LT−1=MbL−bT−2b⋅MaL−3a=Mb+aL−b−3aT−2b
Now, we equate the dimensions on both sides:
1. For mass (M):
0=b+a(1)
2. For length (L):
1=−b−3a(2)
3. For time (T):
−1=−2b(3)
From equation (3):
−1=−2b⟹b=12
0=12+a⟹a=−12
Thus, the values of a and b are:
a=−12,b=12
The values of a and b are respectively −12 and 12.
Topper's Solved these Questions
- UNITS AND MEASUREMENTS BOOK - PHYSICS WALLAHCHAPTER - UNITS AND MEASUREMENTS EXERCISE - NEET PAST 5 YEARS QUESTIONS
10 Videos
- UNITS AND MEASUREMENTS BOOK - PHYSICS WALLAHCHAPTER - UNITS AND MEASUREMENTS EXERCISE - NEET PAST 5 YEARS QUESTIONS
10 Videos
- THERMODYNAMICSBOOK - PHYSICS WALLAHCHAPTER - THERMODYNAMICSEXERCISE - NEET Past 5 Years Questions
14 Videos
- WAVE OPTICSBOOK - PHYSICS WALLAHCHAPTER - WAVE OPTICSEXERCISE - Neet Past 5 Years Questions
16 Videos
Similar Questions
Knowledge Check
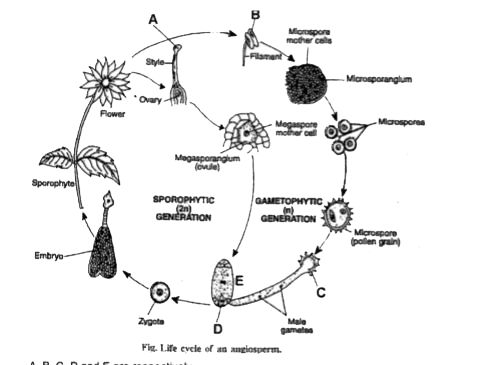
A, B, C, D and E are respectively -AStigma, Anther, Male gametophyte, Egg and Female gametophyteBStigma, Anther, Female gametophyte, Egg and Male gametophyteCStigma, Anther, Male gametophyte, Fertilized egg and Female gametophyteDStigma, Anther, Embryo sac, Egg and Female gametophyteThe wave velocity v, in a medium of elasticity E and density d, is given by
Av=EdBv=√EdCv=√dEDv=√EdThe speed V of sound wave in a fluid having bulk moduluts B and density P is
AV=BpBV=PB,CV=√BpDV=√PB
If v,p and E denote velocity, lenear momentum and KE of the paritcle respectively, then
View SolutionFor the equation FpropA^(a)v^(b)d^©, where F is the force, A is the area V is the velocity and d is the density, the values of a,b and c are, respectively.
View SolutionFor the equation F=Aavbdc where F is force, A is area, v si velocity and d is density with the dimensional anaysis gives the following values for the exponents.
View SolutionThe velocity of sound in air (V) pressure (P) and density of air (d) are related as Vαpxdy. The values of x and y respectively are
View SolutionThe velocity of sound in air (V) pressure (P) and density of air (d) are related as Vαpxdy. The values of x and y respectively are
View Solution