Let be any vector. Another vector which is normal to is :
The correct Answer is:C
To find a vector →B that is normal (perpendicular) to the vector →A=^iAcosθ+^jAsinθ, we can follow these steps:
Step 1: Understand the components of vector →A
The vector →A can be expressed in terms of its components along the x-axis and y-axis:
- The x-component is Ax=Acosθ
- The y-component is Ay=Asinθ
Step 2: Identify the condition for perpendicularity
Two vectors →A and →B are perpendicular if their dot product is zero:
→A⋅→B=0
Step 3: Express vector →B
Let’s assume vector →B has components Bx and By:
→B=^iBx+^jBy
Step 4: Set up the dot product equation
The dot product of →A and →B is given by:
→A⋅→B=(Acosθ)(Bx)+(Asinθ)(By)=0
Step 5: Solve for By in terms of Bx
Rearranging the equation gives:
Acosθ⋅Bx+Asinθ⋅By=0
Dividing through by A (assuming A≠0):
cosθ⋅Bx+sinθ⋅By=0
From this, we can express By in terms of Bx:
By=−cosθsinθBx=−Bxcotθ
Step 6: Choose a specific value for Bx
To simplify, we can choose Bx=1:
By=−cotθ
Step 7: Write the final expression for vector →B
Thus, the vector →B that is perpendicular to →A can be expressed as:
→B=^i(1)+^j(−cotθ)=^i−^jcotθ
Final Answer
The vector →B that is normal to →A is:
→B=^i−^jcotθ
---
The vector →A can be expressed in terms of its components along the x-axis and y-axis:
- The x-component is Ax=Acosθ
- The y-component is Ay=Asinθ
Two vectors →A and →B are perpendicular if their dot product is zero:
→A⋅→B=0
Let’s assume vector →B has components Bx and By:
→B=^iBx+^jBy
The dot product of →A and →B is given by:
→A⋅→B=(Acosθ)(Bx)+(Asinθ)(By)=0
Rearranging the equation gives:
Acosθ⋅Bx+Asinθ⋅By=0
Dividing through by A (assuming A≠0):
cosθ⋅Bx+sinθ⋅By=0
From this, we can express By in terms of Bx:
By=−cosθsinθBx=−Bxcotθ
To simplify, we can choose Bx=1:
By=−cotθ
Thus, the vector →B that is perpendicular to →A can be expressed as:
→B=^i(1)+^j(−cotθ)=^i−^jcotθ
The vector →B that is normal to →A is:
→B=^i−^jcotθ
Topper's Solved these Questions
- MOTION IN A PLANE BOOK - PHYSICS WALLAHCHAPTER - MOTION IN A PLANE EXERCISE - LEVEL-2
30 Videos
- MOTION IN A PLANE BOOK - PHYSICS WALLAHCHAPTER - MOTION IN A PLANE EXERCISE - NEET Past 5 years Questions
10 Videos
- MECHANICAL PROPERTIES OF MATTERBOOK - PHYSICS WALLAHCHAPTER - MECHANICAL PROPERTIES OF MATTEREXERCISE - NEET Past 5 Yeats Questions
16 Videos
- MOTION IN A STRAIGHT LINEBOOK - PHYSICS WALLAHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - NEET Past 5 Years Questions
5 Videos
Similar Questions
If ∣∣→a∣∣=3,∣∣∣→b∣∣∣=4,∣∣→c∣∣=5 and every vector →α is perpendicular to the
sum of the other two vectors. Then the value of ∣∣∣→a+→b+→c∣∣∣2 is :
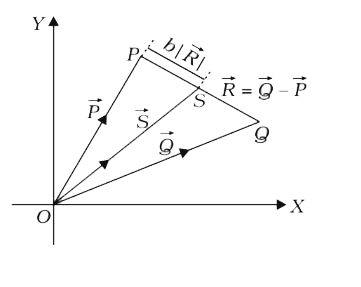
View SolutionThree vectors →P,→Q and →R are shown in the figure. Let S be any point on the vector →R The distance between the point P and S is ∣∣→R∣∣ . The general relation among vectors →P,→Q and →S is :
View Solution
Knowledge Check
Let →A=ˆiAcosθ+ˆjAsinθ, be any vector. Another vector →B which is normal to →A is :-
AˆiBcosθ+ˆjBsinθBˆiBsinθ+ˆjBcosθCˆiBsinθ−ˆjBcosθDˆiAcosθ+ˆjAsinθLet →C=→A+→B then :
A∣∣→C∣∣ is always greater then ∣∣→A∣∣ and ∣∣→C∣∣<∣∣→B∣∣Bit is possible to haveC∣∣→C∣∣ is always equal to ∣∣→A+→B∣∣D∣∣→C∣∣ is never equal to ∣∣→A+→B∣∣The angle between vector (→A−→B) and (→B×→A) is :
A60∘B90∘C120∘D45∘
Dot product of two vectors →A and →B is defined as →A.→B=aBcosϕ , where ϕ is angle between them when they are drawn with tails coinciding. For any two vectors . This means ovsert(→)A.→B=→B.→A that . The scalar product obeys the commutative law of multiplication, the order of the two vectors does not matter. The vector product of two vectors →A and →B also called the cross product, is denoted by →A×→B . As the name suggests, the vector product is itself a vector. →C=→A×→B then C=ABsinθ ,
For non zero vectors →A,→B,→C,∣∣(→A×→B).→C∣∣=∣∣→A∣∣∣∣→B∣∣∣∣→C∣∣ holds if and only if
View SolutionDot product of two vectors →A and →B is defined as →A.→B=aBcosϕ , where ϕ is angle between them when they are drawn with tails coinciding. For any two vectors . This means →A.→B=→B.→A that . The scalar product obeys the commutative law of multiplication, the order of the two vectors does not matter. The vector product of two vectors →A and →B also called the cross product, is denoted by →A×→B . As the name suggests, the vector product is itself a vector. →C=→A×→B then C=ABsinθ ,
→A=ˆi+ˆj−ˆk and →B=2ˆi+3ˆj+5ˆk angle between →A and →B is
View SolutionThe angle between vector (→A×→B) and (→B×→A) is :
View SolutionDot product of two vectors →A and →B is defined as →A.→B=aBcosϕ , where ϕ is angle between them when they are drawn with tails coinciding. For any two vectors . This means →A.→B=→B.→A that . The scalar product obeys the commutative law of multiplication, the order of the two vectors does not matter. The vector product of two vectors →A and →B also called the cross product, is denoted by →A×→B . As the name suggests, the vector product is itself a vector. →C=→A×→B then C=ABsinθ ,
A force →F=3ˆi+cˆj+2ˆk acting on a particle causes a displacement d=4ˆi+2ˆi+3ˆk . If the work done (dot product of force and displacement) is 6J then the value of c is :
View SolutionTwo vectors →A "and" →B have equal in magnitudes. If magnitudes of →A+→B is equal to n
times the magnitude of →A−→B , then the angle
between →Aand→B is :
View Solution
