A system consisting of two masses connected by a massless rod lies along the z-axis. A 9 kg mass is at a distance z =5 m while a 11 kg mass is at a distance 9m. The z coordinate and x-coordinate of the center of mass is (in m )
5,4
72,7.2
7.2,0
2,3
To find the center of mass of the system consisting of two masses connected by a massless rod along the z-axis, we will calculate both the z-coordinate and the x-coordinate of the center of mass.
1. Identify the Given Values:
- Mass m1=9kg at position z1=5m
- Mass m2=11kg at position z2=9m
2. Calculate the Total Mass:
M=m1+m2=9kg+11kg=20kg
3. Calculate the z-coordinate of the Center of Mass:
The formula for the z-coordinate of the center of mass is:
zcom=m1z1+m2z2M
Substituting the values:
zcom=(9kg⋅5m)+(11kg⋅9m)20kg
zcom=45kg m+99kg m20kg=144kg m20kg=7.2m
4. Determine the x-coordinates of the Masses:
Since the masses are connected by a massless rod along the z-axis, both x-coordinates x1 and x2 are 0:
x1=0m,x2=0m
5. Calculate the x-coordinate of the Center of Mass:
The formula for the x-coordinate of the center of mass is:
xcom=m1x1+m2x2M
Substituting the values:
xcom=(9kg⋅0m)+(11kg⋅0m)20kg=020kg=0m
6. Final Result:
- The z-coordinate of the center of mass is 7.2m.
- The x-coordinate of the center of mass is 0m.
Summary:
- z-coordinate of center of mass: 7.2m
- x-coordinate of center of mass: 0m
- Mass m1=9kg at position z1=5m
- Mass m2=11kg at position z2=9m
M=m1+m2=9kg+11kg=20kg
The formula for the z-coordinate of the center of mass is:
zcom=m1z1+m2z2M
Substituting the values:
zcom=(9kg⋅5m)+(11kg⋅9m)20kg
zcom=45kg m+99kg m20kg=144kg m20kg=7.2m
Since the masses are connected by a massless rod along the z-axis, both x-coordinates x1 and x2 are 0:
x1=0m,x2=0m
The formula for the x-coordinate of the center of mass is:
xcom=m1x1+m2x2M
Substituting the values:
xcom=(9kg⋅0m)+(11kg⋅0m)20kg=020kg=0m
- The z-coordinate of the center of mass is 7.2m.
- The x-coordinate of the center of mass is 0m.
- z-coordinate of center of mass: 7.2m
- x-coordinate of center of mass: 0m
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - PHYSICS WALLAHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - LEVEL-2
30 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION BOOK - PHYSICS WALLAHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTION EXERCISE - NEET PAST 5 YEARS QUESTIONS
22 Videos
- SEMICONDUCTOR ELECTRONICS BOOK - PHYSICS WALLAHCHAPTER - SEMICONDUCTOR ELECTRONICS EXERCISE - NEET PAST 5 YEAR QUESTION
23 Videos
- THERMAL PROPERTIES OF MATTER BOOK - PHYSICS WALLAHCHAPTER - THERMAL PROPERTIES OF MATTER EXERCISE - NEET Past 5 Years Questions
12 Videos
Similar Questions
A rigid body consists of a 3kg mass connected to a 2kg mass by a massless rod. The 3kg mass is located at →r1=(2ˆi+5ˆj)m and the 2kg mass at →r2=(4ˆi+2ˆj)m. Find the length of rod and the coordinates of the centre of mass.
View SolutionSix rods of the same mass m and length ? are arranged as shown in figure. Calculate the coordinate of the centre of mass of the system:- У >X
View Solution
Knowledge Check
A system consisting of two masses connected by a massless rod lies along the z-axis. A 9 kg mass is at a distance z =5 m while a 11 kg mass is at a distance 9m. The z coordinate and x-coordinate of the center of mass is (in m )
A5,4B72,7.2C7.2,0D2,3A system consisting of two masses connected by a massless rod lies along the x-axis. A 0.4 kg mass is at a distance x = 2 m while a 0.6 kg mass is at a distance r = 7 m. The x-coordinate of the centre of mass is
A5 mB3.5 mC4.5 mD4 mA system consists of two masses connected by a massless rod lies along x-axis. The distance of centre of mass from O is
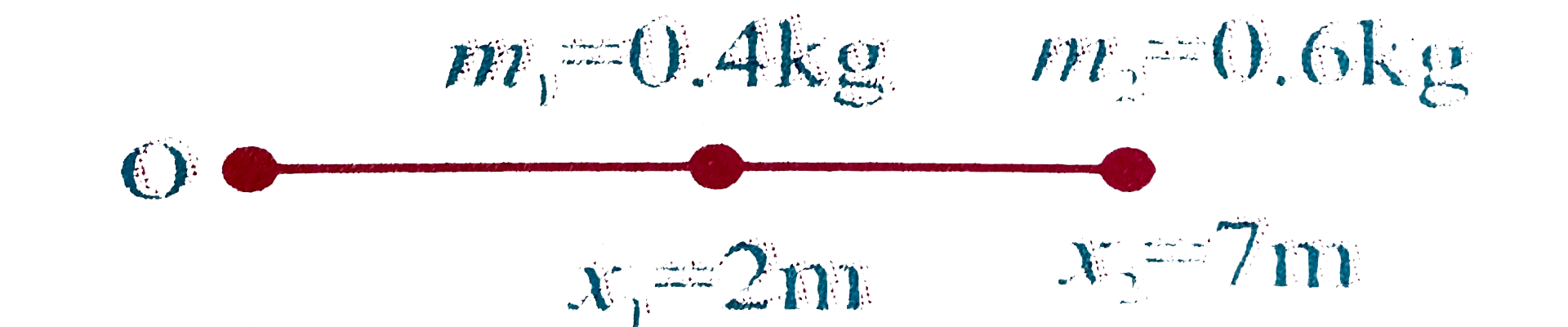 A2mB3mC5mD7m
A2mB3mC5mD7m
Three masses 2 kg , 3kg and 4kg are lying at the corners of an equilateral triangle of side I. The X coordinate of center of mass is
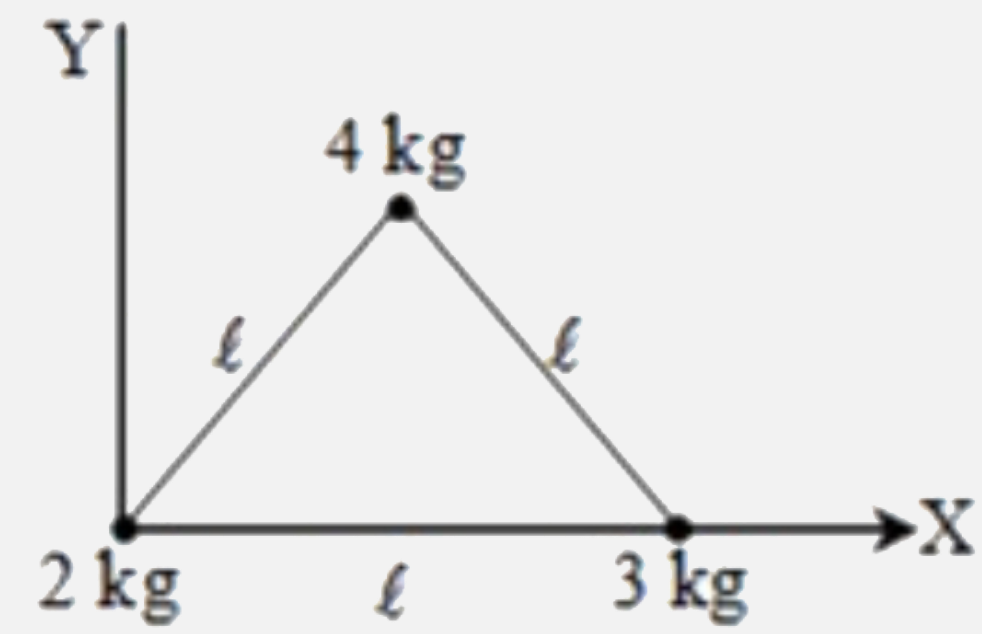
View SolutionA system consisting of two masses connected by a massles rod, lies along the X axis. A body of mass 0.4 kg is kept at a distnce x=2m and another body of mass 0.6 kg is kept at the distance x=6 m from the origin. What is the x-coordinate of the centre of mass?
View SolutionTwo point masses m and M are separated bya distance L . The distance of the centre of mass of the system from m is
View SolutionTwo point masses m and M are separated by a distance L . The distance of the centre of mass of the system from m is
View SolutionFigure shows a composite system of two uniform rods of lengths as indicated. Then the coordinate of the center of mass of the system of rods are

View Solution
