If λ1,λ2,λ3 are the wavelengths of the waves giving resonance in the fundamental, first and second overtone modes respecively in a open organ pipe, then the ratio of the wavelengths λ1:λ2:λ3, is :
A
1:2:3
B
1:3:5
C
1:1/2:1/3
D
1:1/3:1/5
Video Solution
Text Solution
The correct Answer is:C
n1:n2:n3=1:2:3
Vλ1:Vλ2:Vλ3=1:2:3
λ1:λ2:λ3=1:12:13
|
Topper's Solved these Questions
- WAVESBOOK - PHYSICS WALLAHCHAPTER - WAVESEXERCISE - NEET PAST 4 YEARS QUESTIONS
15 Videos
- WAVESBOOK - PHYSICS WALLAHCHAPTER - WAVESEXERCISE - NEET PAST 4 YEARS QUESTIONS
15 Videos
- WAVE OPTICSBOOK - PHYSICS WALLAHCHAPTER - WAVE OPTICSEXERCISE - Neet Past 5 Years Questions
16 Videos
- WORK, ENERGY AND POWERBOOK - PHYSICS WALLAHCHAPTER - WORK, ENERGY AND POWEREXERCISE - NEET Past 5 Years Questions
16 Videos
Similar Questions
Knowledge Check
If λ1,λ2,λ3 are the wavelengths of the waves giving resonance in the fundamental, first and second overtone modes respecively in a open organ pipe, then the ratio of the wavelengths λ1:λ2:λ3, is :
A1:2:3B1:3:5C1:1/2:1/3D1:1/3:1/5If λ1,λ2andλ3 are the wavelengths of the wave giving resonance with the fundamental, first and second overtones respectively of a closed organ pipe Then the ratio of wavelength λ1,λ2andλ3 is
A1:2:3B1:13:15C1:3:5D5:3:1If λ1,λ2andλ3 are the wavelength of the waves giving resonance to the fundamental, first and second overtone modes respectively in a string fixed at both ends. The ratio of the wavelengths λ1:λ2:λ3 is
A1:2:3B1:3:5C1:12:13D1:13:15
Some energy levels of a molecule are shown in the fig. The ratio of the wavelengths r=λ1/λ2, is given by
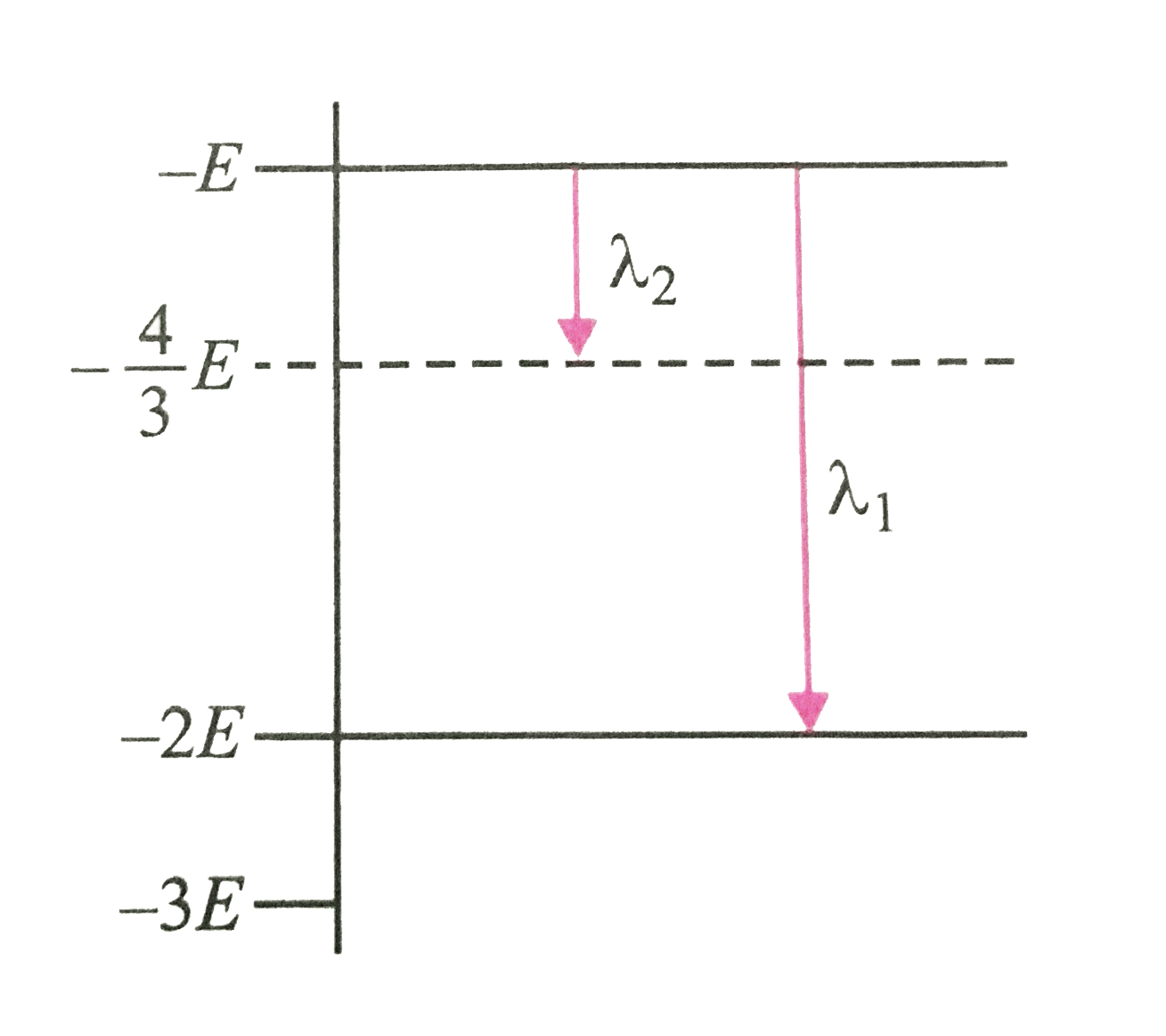
View SolutionThree energy levels P,Q,R of a certain atom are such that EP<EQ<ER. Ifλ1,λ2andλ3 are the wave length of radiation to transition R→Q,Q→P and R→P respectively . The correct relationship between λ1,λ2and,λ3 is
View SolutionThe wavelength of electron waves in two orbits (λ1:λ2)
View Solutionif λv',λx and λm represent the wavelengths of visible light X-rays and microwaves respectively then:
View SolutionIf λ1andλ2 are the wavelength of the first members of the Lyman and Paschen series, respectively , then λ1λ2 is
View Solution
