Three charges q1,q2,q3 each equal to q placed at the vertices of an equilateral triangle of side l . What will be the force on a charge Q placed at the centroid of triangle ?
4N
5N
10N
Zero
The correct Answer is:D
To find the force on a charge Q placed at the centroid of an equilateral triangle formed by three charges q1,q2,q3 (each equal to q), we can follow these steps:
Step 1: Understand the Configuration
We have three charges q1,q2,q3 placed at the vertices of an equilateral triangle with side length l. The centroid of the triangle is the point where the three medians intersect, and it is equidistant from all three vertices.
Step 2: Calculate the Distance from the Centroid to Each Charge
For an equilateral triangle, the distance from the centroid to any vertex (let's denote it as AO) can be calculated as:
AO=23×l√32=l√33
This is derived from the property of centroids in an equilateral triangle.
Step 3: Calculate the Force Exerted by Each Charge on Charge Q
Using Coulomb's law, the force F exerted by a charge q on a charge Q at a distance r is given by:
F=kqQr2
where k=14πϵ0.
Substituting r=AO=l√33:
F=kqQ(l√33)2=kqQl2⋅39=9kqQ3l2=3kqQl2
Step 4: Determine the Direction of Each Force
Since all three charges q1,q2,q3 are positive, the forces F1,F2,F3 acting on charge Q will be directed away from each charge towards the centroid.
Step 5: Calculate the Net Force
The forces F1,F2,F3 form angles of 120∘ with each other due to the symmetry of the equilateral triangle.
Using the vector sum of forces:
- Let F1 be directed along the negative x-axis.
- F2 and F3 will be at 120∘ and 240∘ respectively.
Using the cosine rule to find the resultant of F2 and F3:
Fnet=√F22+F23+2F2F3cos(120∘)
Since F2=F3, we can denote F2=F3=F:
Fnet=√F2+F2+2F2(−12)=√2F2−F2=√F2=F
Thus, the resultant force from F2 and F3 will be equal in magnitude to F1 but in the opposite direction.
Step 6: Conclusion
Since the forces F1,F2,F3 are equal in magnitude and symmetrically arranged, they will cancel each other out. Therefore, the net force on charge Q at the centroid is:
Net Force=0
We have three charges q1,q2,q3 placed at the vertices of an equilateral triangle with side length l. The centroid of the triangle is the point where the three medians intersect, and it is equidistant from all three vertices.
For an equilateral triangle, the distance from the centroid to any vertex (let's denote it as AO) can be calculated as:
AO=23×l√32=l√33
This is derived from the property of centroids in an equilateral triangle.
Using Coulomb's law, the force F exerted by a charge q on a charge Q at a distance r is given by:
F=kqQr2
where k=14πϵ0.
F=kqQ(l√33)2=kqQl2⋅39=9kqQ3l2=3kqQl2
Since all three charges q1,q2,q3 are positive, the forces F1,F2,F3 acting on charge Q will be directed away from each charge towards the centroid.
The forces F1,F2,F3 form angles of 120∘ with each other due to the symmetry of the equilateral triangle.
- Let F1 be directed along the negative x-axis.
- F2 and F3 will be at 120∘ and 240∘ respectively.
Fnet=√F22+F23+2F2F3cos(120∘)
Since F2=F3, we can denote F2=F3=F:
Fnet=√F2+F2+2F2(−12)=√2F2−F2=√F2=F
Thus, the resultant force from F2 and F3 will be equal in magnitude to F1 but in the opposite direction.
Since the forces F1,F2,F3 are equal in magnitude and symmetrically arranged, they will cancel each other out. Therefore, the net force on charge Q at the centroid is:
Net Force=0
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS BOOK - PHYSICS WALLAHCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - LEVEL - 2
29 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - PHYSICS WALLAHCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - NEET PAST 5 YEARS QUESTIONS
7 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - PHYSICS WALLAHCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Neet past 5 years questions
16 Videos
- ELECTROMAGNETIC INDUCTION BOOK - PHYSICS WALLAHCHAPTER - ELECTROMAGNETIC INDUCTION EXERCISE - NEET PAST 5 YEARS QUESTIONS
10 Videos
Similar Questions
Consider three charges q1,q2 and q3 each equal to q at the vertices of an equilateral triangle of side 'l' what is the force on any charge due to remaining charges.
View SolutionConsider three charges q1,q2 and q3 each equal to q at the verticles of an equilateral triangle of side 'l' what is the force on any charge due to remianing charges.
View Solution
Knowledge Check
Three charge −q,+q and −q are placed at the cornors of an equilateral triangle of side a The resultant electric froce an a charge +q placed at a the centroid O of the triangle is
A3q24πε0a2Bq24πε0a2Cq22πε0a2D3q22πε0a2Three equal charges Q are placed at the three vertices of an equilateral triangle. What should be the va,ue of a charge, that when placed at the centroid, reduces the interaction energy of the system to zero ?
A−Q2B−Q3C−Q2√3D−Q√3Three charges 2q,−q,and−q are located at the vertices of an equilateral triangle. At the center of the triangle,
Athe field is zero but potential is nonzero.Bthe field is nonzero but potential is zero.Cboth field and potential are zero.Dboth field and potential are nonzero.
Consider the charges q,q and -q placed at the vertices of an equilateral triangle of each side l. What is the force on each charge ?
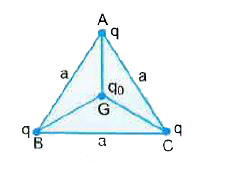
View SolutionThree identical charges of q each are placed at the three verticess of an equilateral triangle ABC of side a, Electrostatic force experienced by a point charge q0 situated at the centroid G of triangle is ___________
View SolutionThree point charges q are placed at three vertices of an equilateral triangle of side a. Find magnitude of electric force on any charge due to the other two.
View SolutionThree equal charges Q are placed at the three corners of an equilateral triangle of side length a. Work done in shifting a charge q from infinity to the centroid of the triangle is
View SolutionThree charges each of value q are placed at the corners of an equilateral triangle. A fourth charge Q is placed at the centre of the triangle. If Q=−q:
View Solution