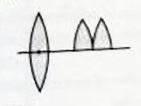
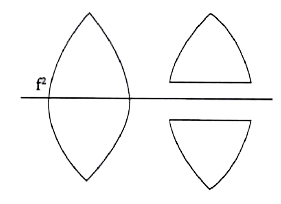
A lens is cut from from the optical centre along the principal axis and the two parts of the lens are placed sideways as shown in figure. Then the new focal length of the combination :
Remain the same
Becomes double
Become half
Become triple
The correct Answer is:C
New focal length of the lends become half .
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRUMENTS BOOK - PHYSICS WALLAHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTS EXERCISE - NEET PAST 5 YEARS QUESTIONS
16 Videos
- RAY OPTICS AND OPTICAL INSTRUMENTS BOOK - PHYSICS WALLAHCHAPTER - RAY OPTICS AND OPTICAL INSTRUMENTS EXERCISE - NEET PAST 5 YEARS QUESTIONS
16 Videos
- OSCILLATIONS BOOK - PHYSICS WALLAHCHAPTER - OSCILLATIONS EXERCISE - NEET PAST 5 YEARS QUESTIONS
5 Videos
- SEMICONDUCTOR ELECTRONICS BOOK - PHYSICS WALLAHCHAPTER - SEMICONDUCTOR ELECTRONICS EXERCISE - NEET PAST 5 YEAR QUESTION
23 Videos
Similar Questions
The power of a plano-convex lens is P. If this lens is cut longitudinally along its principal axis into two equal parts and then they are joined as given in the figure. The power of combination will be :

View SolutionA symmetrical converging convex lens of focal length 10cm & diverging concave symmetrical lens of focal length −20cm are cut from the middle and perpendicularly and symmetrically to their principal axis. The parts thus obtained are arrenged as shown in the figure. Find the focal length (in cm) of this arragement
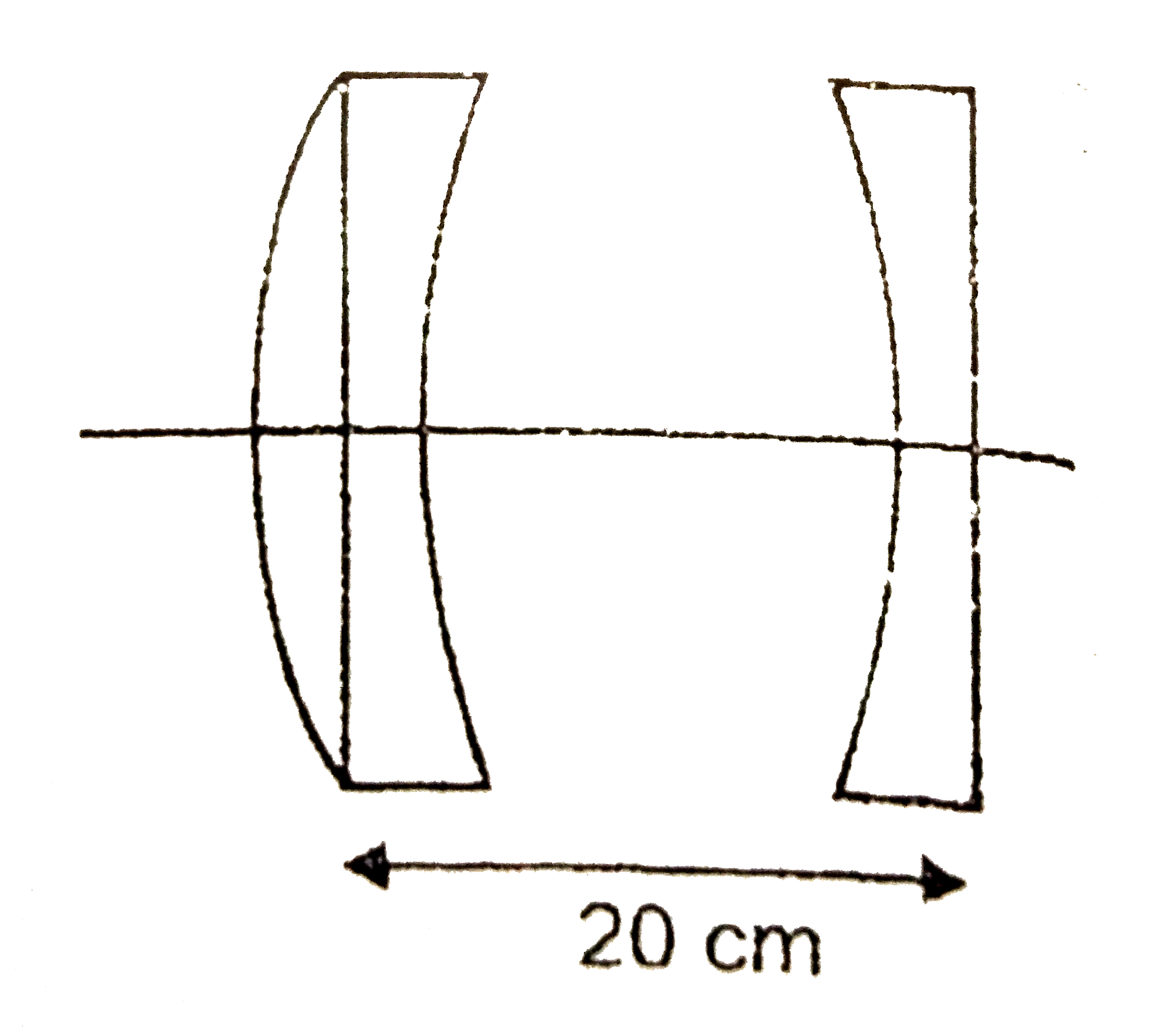
View Solution
Knowledge Check
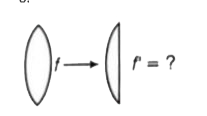
If the bio-convex lens is cut as shown in the figure, the new focal length f' isA2fBfC(f)/(2)DInfiniteIf the bio-convex lens is cut as shown in the figure, the new foacal length f' is
 A2fBfCf/2Dinfinite
A2fBfCf/2DinfiniteA convex lens has a focal length f. It is cut into two parts along the dotted line as shown in figure. The focal length of each part will be
 Af2BfC32fD2f
Af2BfC32fD2f
A symmetrical converging convex lens of focal length 10cm & diverging concave symmetrical lens of focal length −20cm are cut from the middle and perpendicularly and symmetrically to their principal axis. The parts thus obtained are arrenged as shown in the figure. Find the focal length (in cm) of this arragement
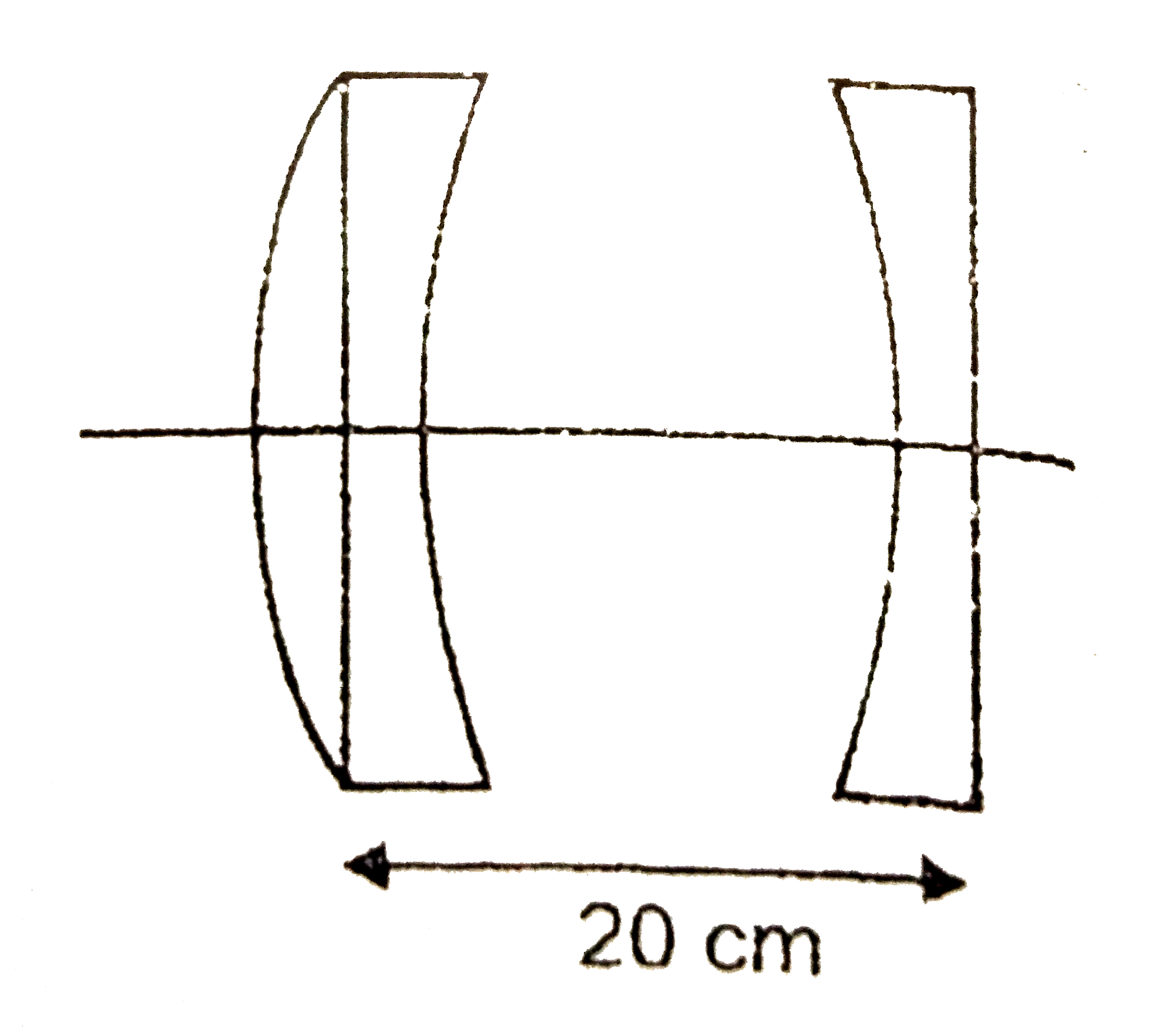
View SolutionA thin double convex lens of focal length f is broken into two equal halves at the axis. The two halves are combined as shown in figure. What is the focal length of combination in (ii) and (iii).
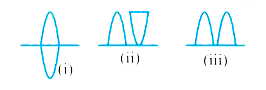
View SolutionA symmetrical biconvex lens of focal length f is cut into four identical pieces along its principal axis and to the perpendicular to principal axis. The focal length of one of four pieces is
View SolutionIf a symmetrical convex lens of focal length 'f is cut into two parts along the principal axis as shown in the figure, the focal length of each part will be:
View SolutionA convex lens has a focal length f. It is cut into two parts along the dotted line as shown in figure. The focal length of each part will be

View Solution
