When the distance of a point light source from a photocell is r1, photoelectric current is I1, If the distance becomes r2, then the current is I2, The ratio (I1:I2) is equal to
r22:r21
r2:r1
r21:r22
r1:r2
The correct Answer is:A
To solve the problem, we need to find the ratio of photoelectric currents I1 and I2 when the distances from a point light source to a photocell change from r1 to r2.
1. Understanding the Relationship:
The photoelectric current I is proportional to the intensity of light I. Therefore, we can write:
I∝Intensity
2. Intensity of Light from a Point Source:
The intensity I of light from a point source is given by the formula:
I=PA
where P is the power of the light source and A is the area over which the light is distributed.
3. Calculating the Area:
For a point source, the area A at a distance r is the surface area of a sphere:
A=4πr2
Therefore, the intensity at a distance r can be expressed as:
I=P4πr2
4. Finding Intensities at Distances r1 and r2:
- At distance r1:
I1=P4πr21
- At distance r2:
I2=P4πr22
5. Calculating the Ratio of Intensities:
To find the ratio I1I2:
I1I2=P4πr21P4πr22=r22r21
6. Expressing the Ratio of Currents:
Since I∝Intensity, we can say:
I1I2=r22r21
7. Final Ratio:
Thus, the ratio of photoelectric currents I1:I2 can be expressed as:
I1:I2=r22:r21
Conclusion:
The final answer is:
(I1:I2)=(r22:r21)
The photoelectric current I is proportional to the intensity of light I. Therefore, we can write:
I∝Intensity
The intensity I of light from a point source is given by the formula:
I=PA
where P is the power of the light source and A is the area over which the light is distributed.
For a point source, the area A at a distance r is the surface area of a sphere:
A=4πr2
Therefore, the intensity at a distance r can be expressed as:
I=P4πr2
- At distance r1:
I1=P4πr21
- At distance r2:
I2=P4πr22
To find the ratio I1I2:
I1I2=P4πr21P4πr22=r22r21
Since I∝Intensity, we can say:
I1I2=r22r21
Thus, the ratio of photoelectric currents I1:I2 can be expressed as:
I1:I2=r22:r21
The final answer is:
(I1:I2)=(r22:r21)
Topper's Solved these Questions
- DUAL NATURE OF RADIATION AND MATTERBOOK - PHYSICS WALLAHCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - Neet past 5 years questions
16 Videos
- CURRENT ELECTRICITYBOOK - PHYSICS WALLAHCHAPTER - CURRENT ELECTRICITYEXERCISE - NEET Past 5 Years Questions
23 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - PHYSICS WALLAHCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - NEET PAST 5 YEARS QUESTIONS
7 Videos
Similar Questions
A solid sphere of mass M and radius R is surrounded by a concentric shell of equal mass M and radius 3R. The gravitational field at a point P1 at a distance r1=2R from the centre is I1 and a point P2at distance r2=4R from the centre is I2 The ratio I2I1
View SolutionIf I(r)=r(r2−1), then n∑r=21I(r) is equal to
View Solution
Knowledge Check
If the distance of 100 Watt lamp is increased from a photocell, the saturation current i in the photo cell varies with distance d as
Ai∝d2Bi∝dCi∝d−1Di∝d−2Find the current I1, I2, & I3, in the circuit.
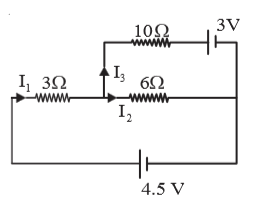 A12,12,1B1,1,2C12,12,3D12,12,0
A12,12,1B1,1,2C12,12,3D12,12,0In the circuit shown, the currents i1 and i2 are
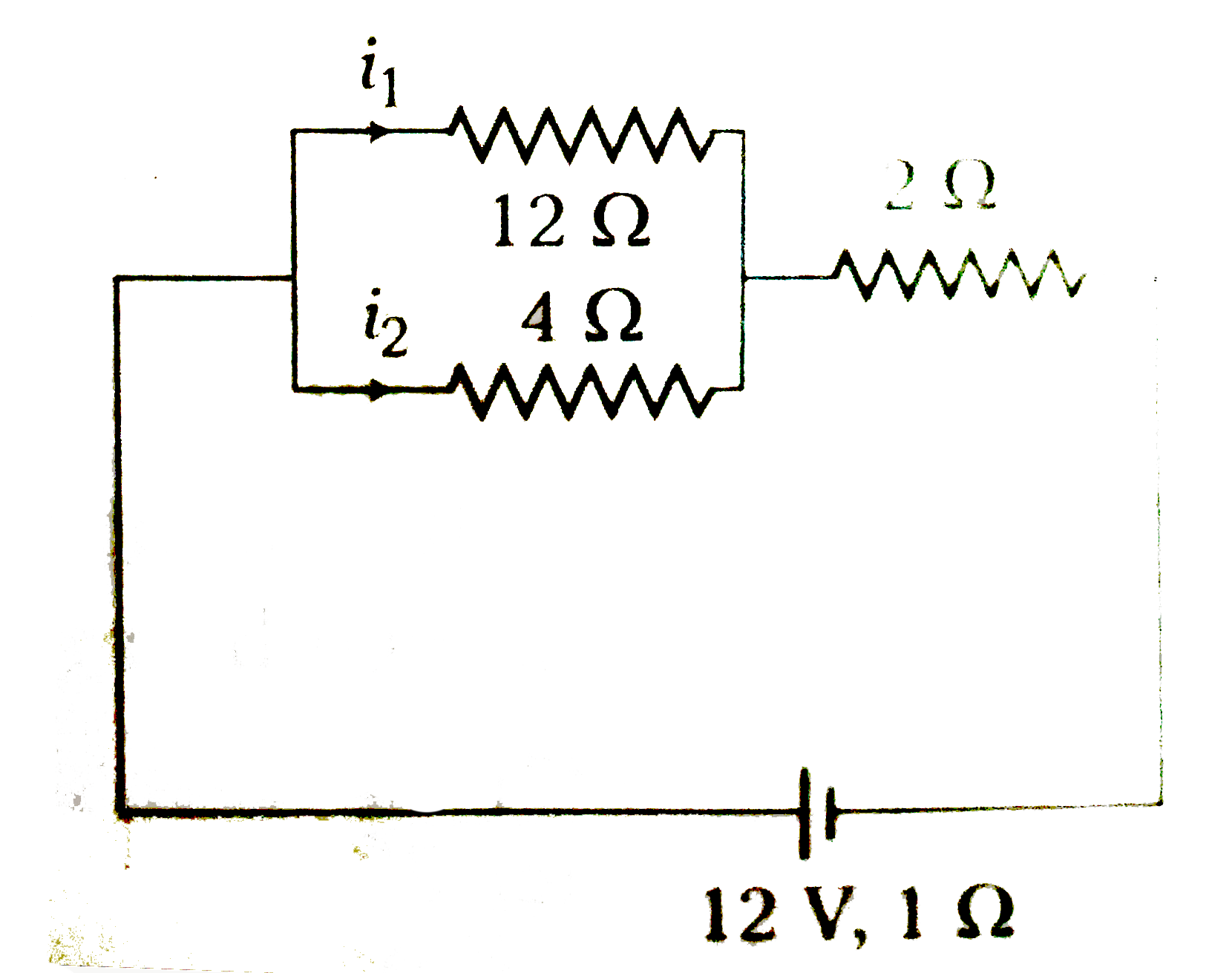 Ai1=1.5A,i2=0.5ABi1=0.5A,i2=1.5ACi1=1A.i2=3ADi1=3A,i2=1A
Ai1=1.5A,i2=0.5ABi1=0.5A,i2=1.5ACi1=1A.i2=3ADi1=3A,i2=1A
In the circuit shown, current through the resistance2Ω isi1 and current through the resistance30Ω is i2. The ratio i1i2 is equal to
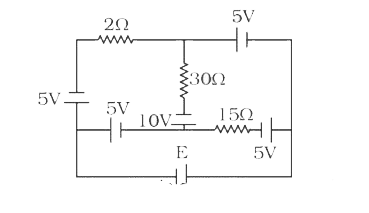
View Solution
Determine the currents I1,I2andI3 from the network shown in figure.
View SolutionIn the circuit shown, the value of currents I1,I2andI3 are
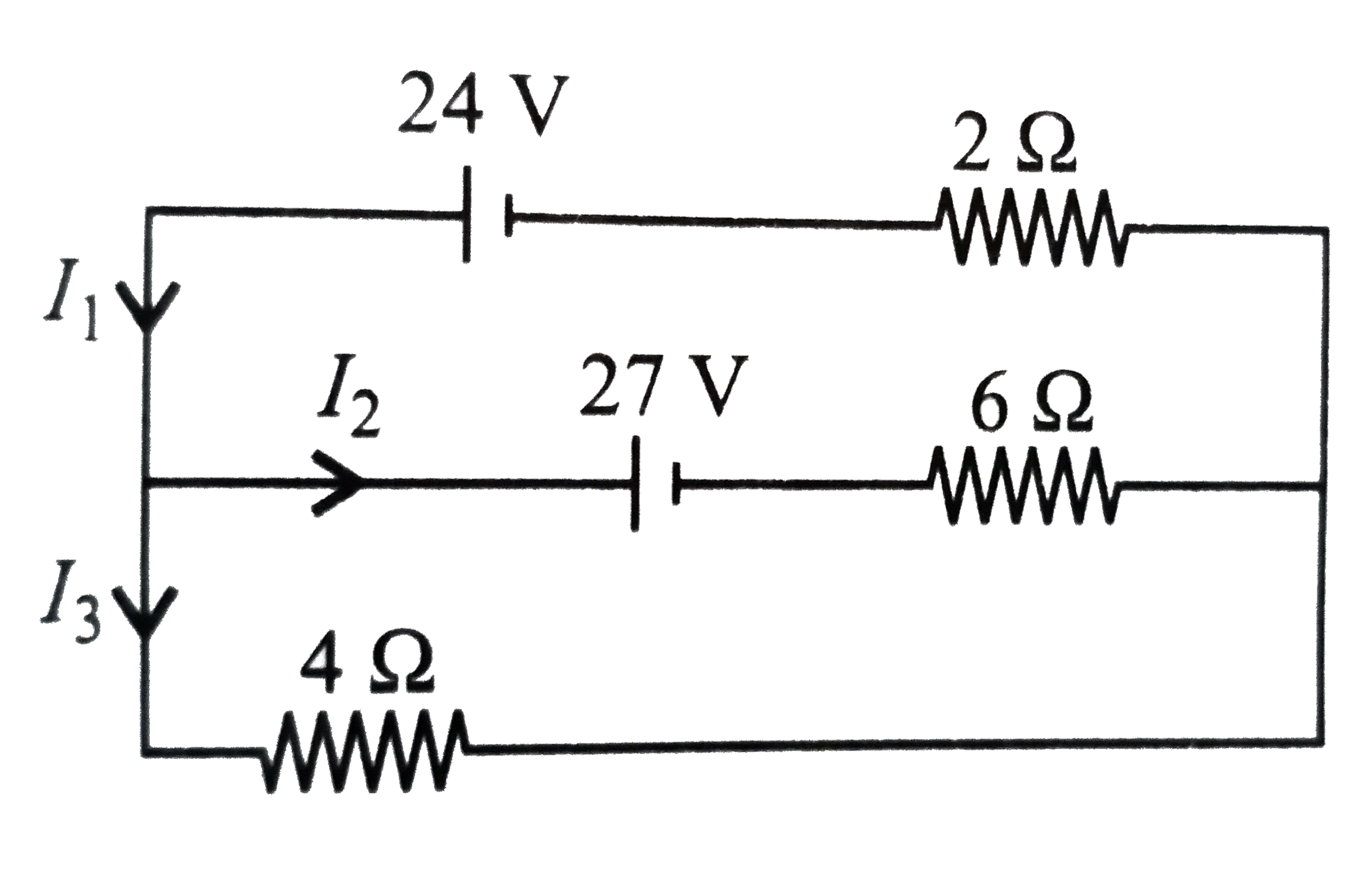
View SolutionIn the given circuit currents I1 and I2 are
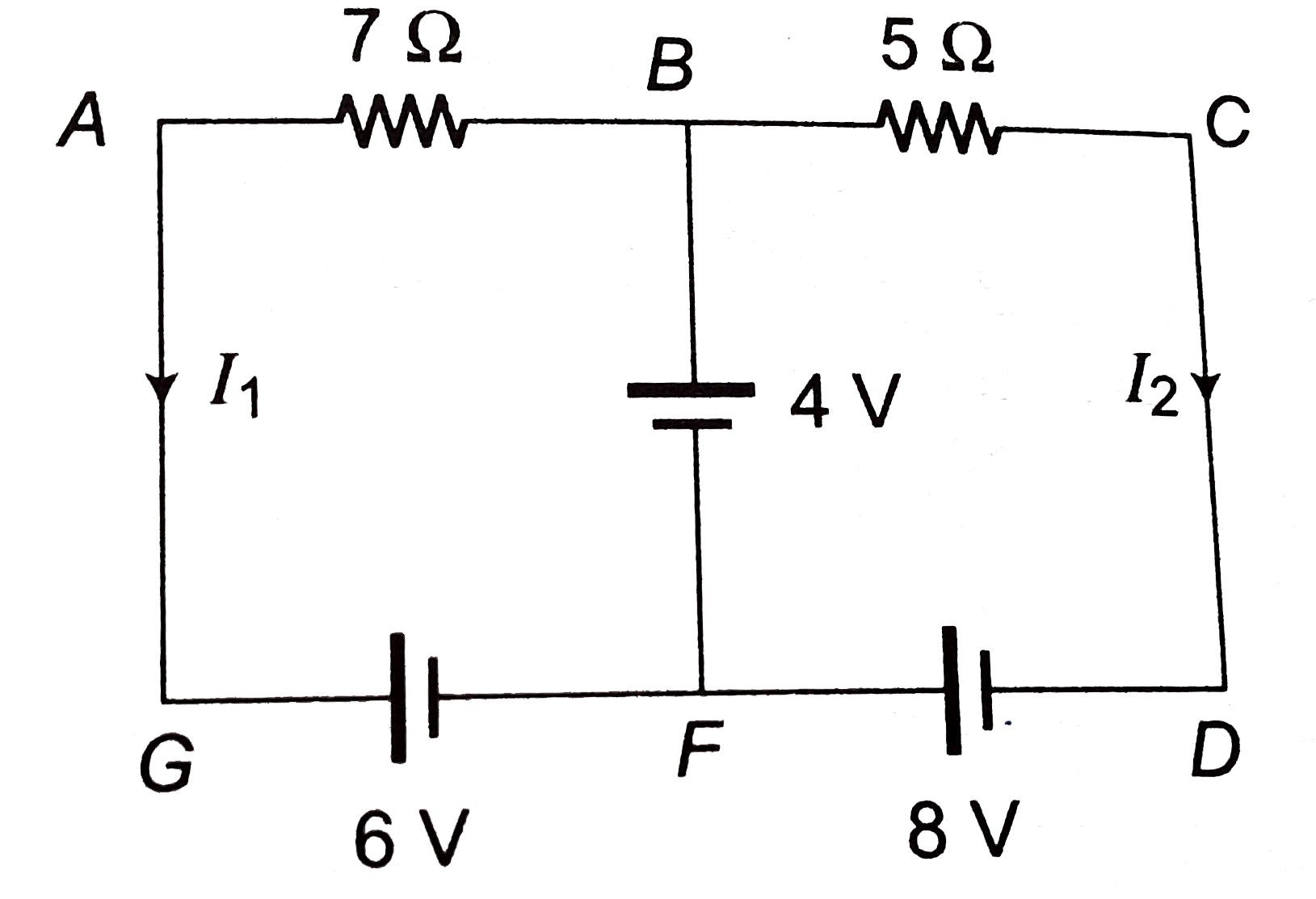 .
.
View SolutionAssertion: If an inductor coil is connected to DC source, the current supplied by it is I1. If the same coil is connected with an AC source of same voltage. Then current is I2, then I2<I1.
Reason: In AC circuit, inductor coil offers more resistance.
View Solution
