Derive an expression at a convex spherical surface when light travels from rarer to denser medium and image formed is (a) real and (b) virtual.
Text Solution
(a) Real image A refracting surface which forms a part of a sphere of transparent refracting material is called a spherical refracting surface.

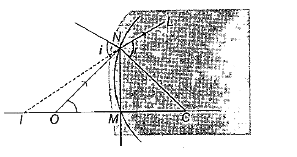
The above figure shows the geometry of formation of image I of an object O and the principle axis of a spherical surface with centre of curvature C and radius of curvature R.
Assumptions
(i) The aperture of the surface is small as compared to other distances involved.
(ii) NM will be taken to be nearly equal to the length of the perpendicular from the point N on the principle axis.
tan∠NOM=NMOM
tan∠NCM=MNMC
tan∠NIM=MNMI
For small angles, tanθ=θ
So, ∠NOM=MNOM,∠NCM=MNMN,
∠NIM=MNMI
For ΔNOC, i is the exterior angle.
∴i=∠NOM+∠NCM
i=MNOM+MNMC ...(i)
For ΔNIC,∠NCM is the exterior angle.
∴∠NCM=r+∠NIM
or r=∠NCM−∠NIM
i.e. r=MNMC−MNMI ...(ii)
By Snell.s law,
μ1sini=μ2sinr
For small angles,
μ1i=μ2r
Substituting the values of i and r from Eqs. (i) and (ii), we obtain
μ1(MNOM+MNMC)=μ2(MNMC−MNMI)
or μ1OM+μ2MI=μ2−μ1MC ...(iii)
Applying new cartesian sign conventions,
OM=−u,MI=+v,MC=+R
Substituting these values in Eq. (iii), we obtain
μ2v−μ1u=μ2−μ1R
This equation holds for any curved spherical surface.
(b) Virtual Image In ΔNOC, exterior angle,
i=∠NOM+∠NCM
i=MNOM+MNMC ...(i)
In ΔNIC, exterior angle,
∠LNC=r=∠NIM+∠NCM
∴r=MNIM+MNMC ...(ii)
By Snell.s law, μ1sini=μ2sinr
For small angles, μ1i=μ2r
On substituting values of i and r from Eqs. (i) and (ii), we obtain
μ1(MNOM+MNMC)=μ2(MNIM+MNMC)
or μ1OM−μ2IM=μ2−μ1MC ...(iii)
Applying new cartesian sign conventions, OM=−u,MI=−vandMC=+R
On substituting these values in Eq. (iii), we obtain
μ1−u−μ2−v=μ2−μ1R
or μ2v−μ1u=μ2−μ1R
|
Similar Questions
Knowledge Check
When light passes from a denser medium to a rarer medium
AVelocity of light increasesBVelocity of light decreasesCVelocity of light remains unchangedDVelocity of light becomes infinityWhen a light ray enters from a denser medium to a rarer medium.
AThe light ray bends towards the normal.BAngle of incidence is less than angle of refraction.CSpeed of light decreases.DSpeed of light remains unchanged.When light travels from a rarer medium to a denser medium, it ________
Aspeed remains the sameBspeeds down then upCspeeds downDspeeds up
When a ray of light travels obliquely from a rarer medium to a denser medium, it bends away from the normal.
View SolutionLight is travelling from a denser medium to a rarer medim along a normal to the boundary:
View SolutionWhen a ray of light travels from a denser medium to a rarer medium, the ray will :
View SolutionWhen a wave travels from a denser to rarer medium, then
View SolutionWhen a ray of light passes from a denser medium to a rarer medium, the ray …………. .
View Solution
