समीकरण 1−cosθ=sinθsin.θ2 के मूल है।
kπ
2kπ
3kπ
kπ2
The correct Answer is:B
Step by step video, text & image solution for समीकरण 1- cos theta = sin theta sin .(theta)/(2) के मूल है। by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
किसी ग्राहक को एक मोटर साइकिल, जिसका अंकित मूल्य ₹40,000 है, खरीदने के लिए ₹44,800 देने पड़ते हैं। मोटर साइकिल पर बिक्री कर की दर है-
04:11View Solutionनिम्न चित्र में छायांकित भाग का क्षेत्रफल है -
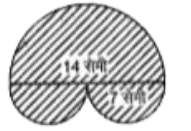 03:13View Solution
03:13View Solution1+cosθ+sinθ1+cosθ−sinθ=1+sinθcosθ
00:54View Solution1- (sin ^ (2) theta) / (1 + cos theta) + (1 + cos theta) / (sin theta) - (sin theta) / (1-cos theta) - (1) / (sec theta)
02:15View Solution(cos^(2)theta(1-cos theta))/(sin^(2)theta(1-sin theta))=(1+sin theta)/(1+cos theta)
04:47View SolutionProve that (1)/(2){(sin theta)/(1+cos theta)+(1+cos theta)/(sin theta)}=(1)/(sin theta)
03:37View Solutionसिद्ध करे की sinθ−cosθ+1sinθ+cosθ−1=1+sinθcosθ
02:09View Solutionसिद्ध करो कि :
sinθ−cosθsinθ+cosθ+sinθ+cosθsinθ−cosθ=22sin2θ−102:48View SolutionProve that 1+cosθsinθ=1+sinθ+cosθ1+sinθ−cosθ
05:03View Solutionsin2θ1−cosθ−cos2θ1−sinθ=cosθ−sinθ
01:28View Solution1+sinθ−cosθ1+sinθ+cosθ+1+sinθ+cosθ1+sinθ−cosθ=
01:29View Solution(sinθ+cosθ)2−1sinθ⋅cosθ
04:38View SolutionEvaluate the following determinants:
(b) ∣∣∣cosθ−sinθsinθcosθ∣∣∣=cosθ(cosθ)−sinθ(−sinθ)=cos2θ+sin2θ=105:32View Solutioncosθ1−sinθ=1+cosθ+sinθ1+cosθ−sinθ
15:50View Solution1-(sin^(2) theta)/(1+cos theta) + (1+cos theta)/(sin theta) - (sin theta)/(1-cos theta) - (1)/(sec theta)=
03:16View Solutionनिम्नलिखित सर्व समिकाओ को सिद्ध करो-
(i) (1−cosθ)(1+cosθ)(1+cot2θ)=1
(ii) (1+sinθ)2+(1−sinθ)2)2cos2θ=1+sinθ21−sin2θ
(iii) cos2θ(1−cosθ)sin2θ(1−sinθ)=1+sinθ1+cosθ
(iv) (sinθ−cosθ)2=1−2sinθ.cosθ
(v) (sinθ+cosθ)2+(sinθ−cosθ)2=2
(vi) (asinθ+bcosθ)2+(acosθ−bsinθ)2=a2+b2
(vii) cos4A+sin4A+2sin2A.cos2A=1
(ix) (cos4θ−sin4θ)=cos2θ−sin2θ=2cos2θ−1
(x) 2cos2θ−cos4θ+sin4θ=1
(xi) 1−2cos2θ+cos4θ=sin4θ
(xii) 1−2sin2θ+sin4θ=cos4θ03:48View Solution

