Find the side of the square having Area equal to 49cm2Solution in Punjabi
The correct Answer is:Side=7 cm
Step by step video & image solution for Find the side of the square having Area equal to 49cm^2 by Maths experts to help you in doubts & scoring excellent marks in Class 8 exams.
Topper's Solved these Questions
Similar Questions
Construct a quadrilateral PQRS where PQ = 4 cm, QR = 6 cm,RS = 5 cm,PS = 5.5 cm and PR = 7 cm.
03:13View SolutionFind the value of Q:
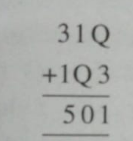 .01:32View Solution
.01:32View SolutionUsing appropriate properties find : −23×35+52−35×16
00:52View SolutionTwo squares have sides xcm and (x+4) . The sum of their areas is 656cm2 . Find the sides of the squares.
01:10View SolutionThe area of a rectangle is 49cm2 and its breadth is 2.8cm. Find the length of the rectangle.
04:47View SolutionThe area of a square of side 14cm is 49cm2 (b) 156cm2 (c) 56cm2 (d) 196 cm2
00:56View SolutionIf area of circle is equal to area of square and side of a square is 23cm then find the radius of circle?
01:01View SolutionA square is drawn with the length of side equal to the diagonal of a cube. If the area of the square is 72075cm2, then find the side of the cube.
01:12View Solutionएक वर्गाकार क्षेत्र का क्षेत्रफल 2304m2है । इस वर्गाकार क्षेत्र की भुजा ज्ञात कीजिए ।
01:14View Solutionवर्ग का क्षेत्रफल निकालिए जबकि भुजा बराबर
6 सेमी02:35View Solutionवर्ग का क्षेत्रफल निकालिए जबकि भुजा बराबर
10 सेमी02:42View Solutionवर्ग का क्षेत्रफल निकालिए जबकि भुजा बराबर
8 मी03:06View SolutionA square and a rectangle have equal area. If side of a square is 24 cm and the length of the rectangle is 32 cm , find
the breadth of the rectangle03:20View SolutionA square and a rectangle have equal area. If side of a square is 24 cm and the length of the rectangle is 32 cm , find
the perimeter of the rectangle.02:27View SolutionFind the area of a circle inscribed in a square of side 28 cm. [Hint: Diameter of the circle is equal to the side of the square]
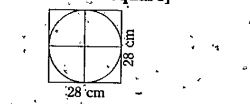 02:15View Solution
02:15View SolutionThe area of a rectangle is equal to the area of a square of side 12 cm. Find the perimeter of the square and all possible rectangles.
03:15View Solution

